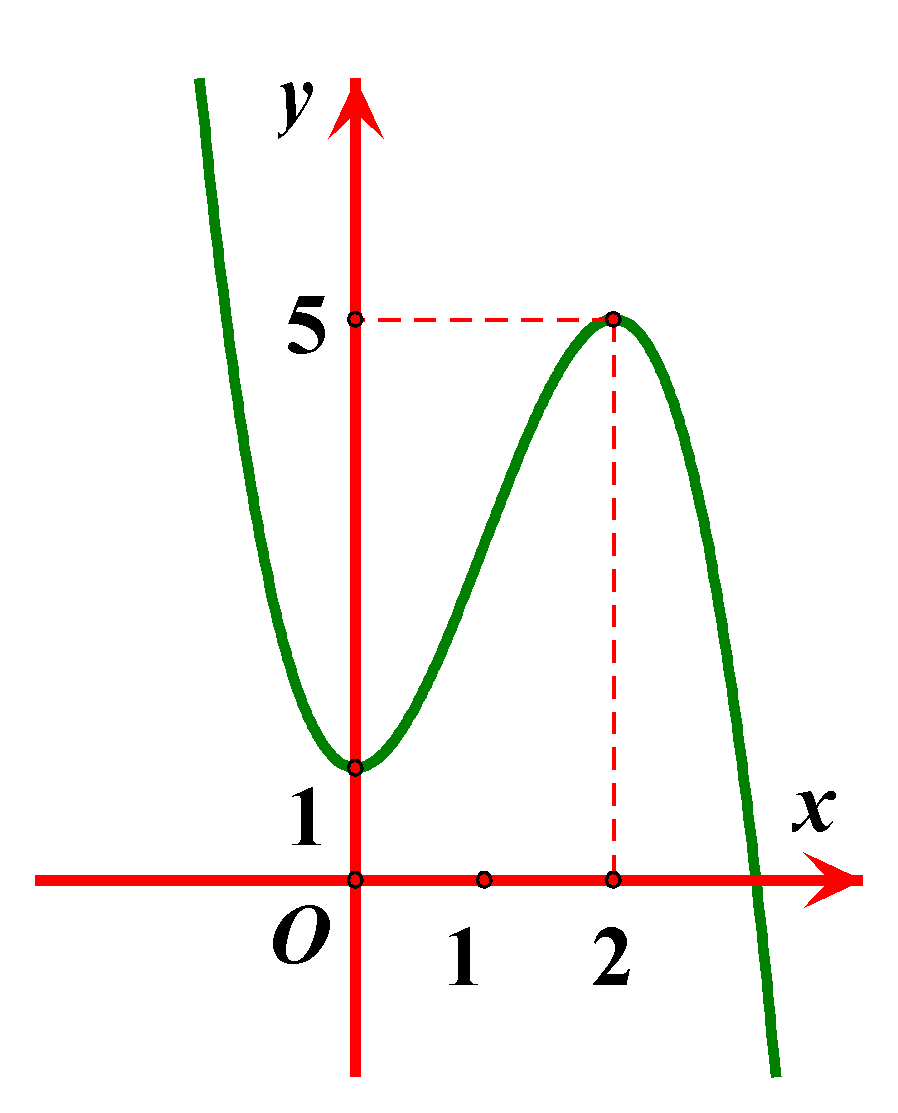
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ:
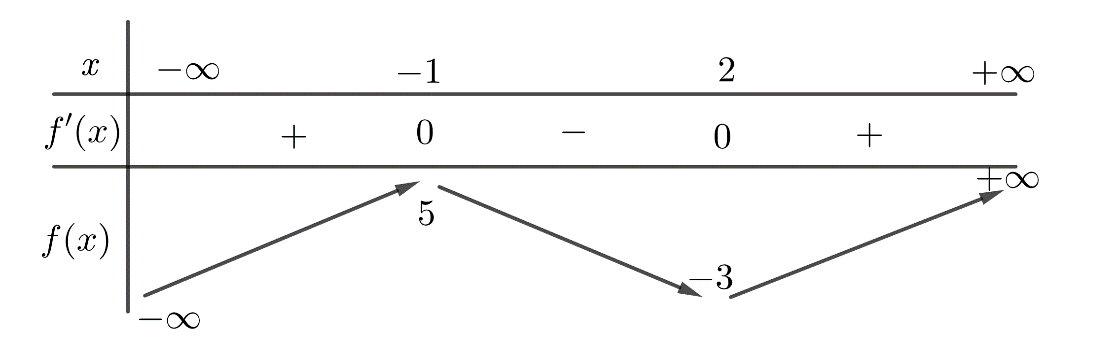
Số giá trị nguyên của tham số \(m\) để hàm số \(g\left( x \right)=f\left[ f\left( x \right)-m+1 \right]\) có đúng \(6\) điểm cực trị là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(g\left( x \right)=f\left[ f\left( x \right)-m+1 \right]\Rightarrow {g}'\left( x \right)={f}'\left( x \right).{f}'\left[ f\left( x \right)-m+1 \right]\)
Khi đó \({g}'\left( x \right)=0\)
\(\Leftrightarrow\) \(\left[ \begin{align} & {f}'\left( x \right)=0 \\ & {f}'\left[ f\left( x \right)-m+1 \right]=0 \\ \end{align} \right.\)
\(\Leftrightarrow \left[ \begin{align} & x=-1 \\ & x=2 \\ & f\left( x \right)-m+1=-1 \\ & f\left( x \right)-m+1=2 \\ \end{align} \right.\)
\(\Leftrightarrow \left[ \begin{align} & x=-1 \\ & x=2 \\ & f\left( x \right)=m-2 \\ & f\left( x \right)=m+1 \\ \end{align} \right.\)
Dựa vào bảng biến thiên, hàm số \(g\left( x \right)\) có 6 điểm cực trị khi
\(\left[ \begin{align} & m-2\le -3<m+1<5 \\ & -3<m-2<5\le m+1 \\ \end{align} \right.\)
\( \left\{ \begin{align} & m\le -1 \\ & -4<m<4 \\ \end{align} \right.\) hoặc \(\left\{ \begin{align} & -1<m<7 \\ & m\ge 4 \\ \end{align} \right. \),
\(\Leftrightarrow \left[ \begin{align} & -4<m\le -1 \\ & 4\le m<7 \\ \end{align} \right.\)
Vậy có 6 giá trị nguyên \(m\) thoả yêu cầu bài toán.
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Nguyễn Kiệm
Câu hỏi liên quan
-
Tập nghiệm của bất phương trình \({{\log }_{3}}\left( x-2 \right)\le 2\) là
-
Cho hàm số \(f\left( x \right)={{x}^{4}}+b{{x}^{2}}+c\left( b,c\in \mathbb{R} \right)\) có đồ thị là đường cong \(\left( C \right)\) và đường thẳng \(\left( d \right):y=g\left( x \right)\) tiếp xúc với \(\left( C \right)\) tại điểm \({{x}_{0}}=1\). Biết \(\left( d \right)\) và \(\left( C \right)\) còn hai điểm chung khác có hoành độ là \({{x}_{1}},{{x}_{2}}\left( {{x}_{1}}<{{x}_{2}} \right)\) và \(\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{\frac{g\left( x \right)-f\left( x \right)}{{{\left( x-1 \right)}^{2}}}dx=\frac{4}{3}}\). Tính diện tích hình phẳng giới hạn bởi đường cong \(\left( C \right)\) và đường thẳng \(\left( d \right)\).
-
Một nguyên hàm của hàm số \(f\left( x \right)=\sin \left( 2x-\frac{\pi }{3} \right)\) là
-
Có bao nhiêu giá trị nguyên \({b>1}\) để với mỗi giá trị của \({b}\) có đúng 5 số nguyên \(a\in \left( -10;10 \right)\) thỏa mãn \({\log _{3} \frac{2 a^{2}+3 a+b}{a^{2}-a+2} \leq a^{2}-6 a+7-b}\).
-
Cho phương trình\({{z}^{2}}+az+2{{a}^{2}}=0\), với \(a\) là số thực dương. Gọi \({{z}_{1}},{{z}_{2}}\) là hai nghiệm phức của phương trình, trong đó \({{z}_{1}}\)có phần ảo dương. Biết rằng \(\left( 2{{z}_{1}}+{{z}_{2}} \right)\overline{{{z}_{1}}}=10+2\sqrt{7}i\). Khẳng định làm sau đây đúng?
-
Cho hình hộp đứng có đáy là hình vuông cạnh bằng \(a,\) độ dài cạnh bên bằng \(3a.\) Thể tích của khối hộp đã cho bằng
-
Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm \(SD\) khi đó \(\sin \left( CM,\left( ABCD \right) \right)\) bằng
-
Tiệm cận đứng của đồ thị hàm số \(y=\frac{2x-1}{x+1}\) là đường thẳng có phương trình
-
Trong không gian \(Oxyz,\) cho hai điểm \(A\left( 1;-2;-3 \right),\,\,B\left( -1;4;1 \right)\) và đường thẳng \(d:\frac{x+2}{1}=\frac{y-2}{-1}=\frac{z+3}{2}.\) Phương trình đường thẳng \(\Delta \) đi qua trung điểm của đoạn \(AB\) và song song với đường thẳng \(d\) là
-
Đồ thị hàm số \(y=\frac{x-4}{2x+2}\) cắt trục tung tại điểm có tung độ bằng
-
Trong không gian \(Oxyz,\)cho mặt phẳng \(\left( P \right):2x-y+z-10=0\) và \(d:\frac{x+2}{2}=\frac{y-1}{1}=\frac{z-1}{-1}.\) Đường thẳng \(\Delta \) cắt \(\left( P \right)\) và đường thẳng \(d\) lần lượt tại \(M\)và \(N\) sao cho \(A\left( 1;3;2 \right)\)là trung điểm của \(MN.\) Tính độ dài đoạn thẳng \(MN.\)
-
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ:
Số điểm cực trị của hàm số đã cho bằng
-
Trong không gian \(Oxyz\), phương trình nào dưới đây là phương trình của mặt cầu tâm \(I\left( 1;\ 0;\ -2 \right),\) bán kính \(R=4?\)
-
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AD=2\sqrt{2},\,\,AB=1,\,\,\)
\(SA=SB,\,\)\(SC=SD.\) Biết rằng hai mặt phẳng \(\left( SAB \right)\) và \(\left( SCD \right)\) vuông góc với nhau và tổng diện tích của hai tam giác \(SAB\) và \(SCD\) bằng \(\sqrt{3}.\) thể tích của khối chóp \(S.ABCD\) bằng
-
Cho hàm số \(y=f\left( x \right)\), hàm số \(y={f}'\left( x \right)\) liên tục trên \(R\) và có đồ thị như hình vẽ.
Bất phương trình \(f\left( x \right)-{{\left( x-1 \right)}^{3}}>m+5x+1\) (với \(m\) là tham số thực) nghiệm đúng với mọi \(x\in \left( 0\,;\,3 \right)\) khi và chỉ khi
-
Trong không gian \(Oxyz,\) mặt phẳng \(\left( \alpha \right):-2x+3y-z+5=0\) đi qua điểm nào dưới đây?
-
Cho hàm số đa thức bậc bốn \(y=f\left( x \right)\), đồ thị của hàm số \(y={f}'\left( 1-x \right)\) là đường cong ở hình vẽ.
Hàm số \(h\left( x \right)=f\left( x \right)-\frac{3}{2}{{x}^{2}}\) đạt giá trị nhỏ nhất trên \(\left[ 0;2 \right]\) tại
-
Cho \(g\left( x \right)={{x}^{2}}-2x-1\) và hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ:
Số nghiệm của phương trình \(f\left[ g\left( x \right) \right]=0\) là
-
Hàm số \(y=\frac{1}{3}{{x}^{3}}-\frac{1}{2}{{x}^{2}}-6x+\frac{5}{6}\) đồng biến trên khoảng
-
Cho hai số phức \({{z}_{1}}=3+i\) và \({{z}_{2}}=2-i.\) Tính \(T=\left| {{z}_{1}}+{{z}_{1}}{{z}_{2}} \right|.\)
