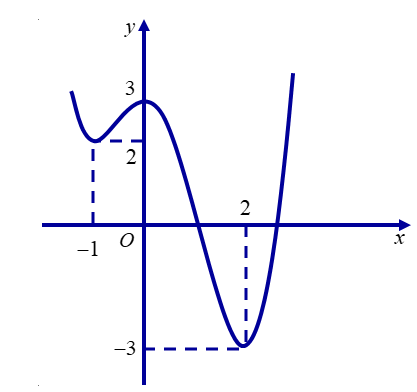
Cho hàm số \(f\left( x \right)\) là hàm số đa thức bậc bốn. Biết \(f\left( 0 \right)=0\) và đồ thị hàm số \(y={f}'\left( x \right)\) có hình vẽ bên dưới.
.PNG)
Tập nghiệm của phương trình \(f\left( \left| 2\sin x-1 \right|-1 \right)=m\) (với \(m\) là tham số) trên đoạn \(\left[ 0;3\pi\right]\) có tất cả bao nhiêu phần tử?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn D
Đồ thị đã cho là đồ thị hàm số bậc ba có hai điểm cực trị \(x=0\) và \(x=2\) nên có dạng \({f}'\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d\).
Lần lượt thay thế các dữ kiện từ hình vẽ, ta được
\(\begin{array}{l} \left\{ \begin{array}{l} d = 2\\ c = 0\\ 3 \cdot a \cdot {2^2} + 2 \cdot b \cdot 2 = 0\\ - {a^3} + b + d = - 2 \end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l} a = 1\\ b = - 3\\ c = 0\\ d = 2 \end{array} \right. \end{array}\)
Suy ra \({f}'\left( x \right)={{x}^{3}}-3{{x}^{2}}+2\)\( \Rightarrow f\left( x \right)=\frac{{{x}^{4}}}{4}-{{x}^{3}}+2x+C\).
Mà \(f\left( 0 \right)=0\)\( \Rightarrow C=0\Rightarrow f\left( x \right)=\frac{{{x}^{4}}}{4}-{{x}^{3}}+2x\).
Ta có \({f}'\left( x \right)=0\)
\(\Leftrightarrow \left[ \begin{align} & x=1 \\ & x=1-\sqrt{3} \\ & x=1+\sqrt{3} \\ \end{align} \right.\)
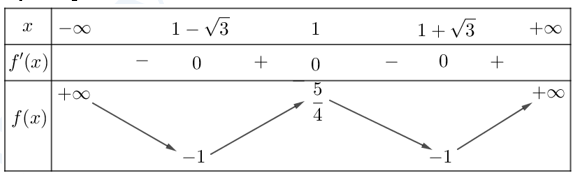
Suy ra bảng biến thiên
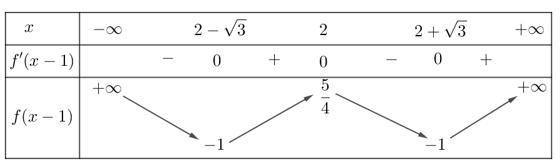
Từ đó ta có bảng biến thiên của \(f\left( x-1 \right)\)
Vì \(-1\le \sin x\le 1,\forall x\in \left[ 0;3\pi\right]\) nên \(0\le \left| 2\sin x-1 \right|\le 3\).
Đặt \(t=\left| 2\sin x-1 \right|\), \(t\in \left[ 0;3 \right]\)
Dựa vào bảng biến thiên, suy ra phương trình \(f\left( t-1 \right)=m\) có tối đa \(2\) nghiệm \(t=h\), \(t=k\).
Do đó
\(\begin{array}{l} \left[ \begin{array}{l} 2\sin x - 1 = \pm h\\ 2\sin x - 1 = \pm k \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} \sin x = \frac{{ \pm h + 1}}{2}\\ \sin x = \frac{{ \pm k + 1}}{2} \end{array} \right. \end{array}\)
Trên \(\left[ 0;3\pi\right]\), mỗi phương trình có nhiều nhất \(4\) nghiệm, do đó phương trình đã cho có nhiều nhất \(16\) nghiệm.
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Lương Thế Vinh
Câu hỏi liên quan
-
Giả sử \(f\left( x \right)\) là hàm có đạo hàm liên tục trên khoảng \(\left( 0;\pi \right)\) và \(f'\left( x \right)\sin x=x+f\left( x \right)\cos x,\,\,\,\forall x\in \left( 0;\pi \right).\) Biết \(f\left( \frac{\pi }{2} \right)=1,\,\,f\left( \frac{\pi }{6} \right)=\frac{1}{12}\left( a+b\ln 2+c\pi \sqrt{3} \right)\), với \(a,\,\,b,\,\,c\) là các số nguyên. Giá trị \(a+b+c\) bằng
-
Cho khối lăng trụ tam giác \(ABC.{A}'{B}'{C}'\)có cạnh \(A{A}'=2a\) và tạo với mặt phẳng đáy một góc bằng \(60{}^\circ \), diện tích tam giác \(ABC\)bằng \({{a}^{2}}\). Thể tích khối lăng trụ \(ABC.{A}'{B}'{C}'\)bằng
-
Cho hàm số \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\) (với \(a,b,c,d\in \mathbb{R}\)) có đồ thị như hình vẽ
.PNG)
Có bao nhiêu số dương trong các số \(a,b,c,d\)?
-
Gọi \({{z}_{1}}\), \({{z}_{2}}\) là các nghiệm phức của phương trình \({{z}^{2}}-3z+5=0\). Môđun của số phức \(\left( 2{{{\bar{z}}}_{1}}-3 \right)\left( 2{{{\bar{z}}}_{2}}-3 \right)\) bằng
-
Trong không gian \(Oxyz\), đường thẳng \(\Delta :\frac{x}{1}=\frac{y-1}{1}=\frac{z}{-1}\) song song với mặt phẳng nào sau đây?
-
Cho khối chóp \({S.ABCD}\) có đáy \({ABCD}\) là hình thoi, \({\widehat{DAB}=60{}^\circ }\), \({AD=a}\), tam giác \({SBC}\) cân tại \({S}\), tam giác \({SCD}\) vuông tại \({C}\), khoảng cách giữa \({SA}\) và \({CD}\) bằng \({\frac{4a}{5}}\). Thể tích của khối chóp đã cho bằng
-
Hàm số \(f\left( x \right)={{x}^{4}}{{\left( x-1 \right)}^{2}}\) có bao nhiêu điểm cực trị?
-
Một tổ học sinh có 12 bạn, gồm 7 nam và 5 nữ. Cần chọn một nhóm 3 học sinh của tổ đó để làm vệ sinh lớp học. Hỏi có bao nhiêu cách chọn sao cho trong nhóm có cả nam và nữ?
-
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):ax+by+cz+7=0\) qua điểm \(A\left( 2;0;1 \right)\), vuông góc với mặt phẳng \(\left( Q \right):3x-y+z+1=0\) và tạo với mặt phẳng \(\left( R \right):x-y+2z-1=0\) một góc \({{60}^{\text{o}}}\). Tổng \(a+b+c\) bằng
-
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Mặt bên \(SAB\) là tam giác đều cạnh \(\sqrt{3}a\), \(ABC\) là tam giác vuông tại \(A\) có cạnh \(AC=a\), góc giữa \(AD\) và \((SAB)\) bằng \(30{}^\circ \). Thể tích khối chóp \(S.ABCD\) bằng
-
Nghiệm của phương trình \({{2}^{x-1}}=8\) là
-
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right):{{x}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+3 \right)}^{2}}=24\) cắt mặt phẳng \(\left( \alpha \right):x+y=0\) theo giao tuyến là đường tròn \(\left( C \right)\). Tìm hoành độ của điểm \(M\) thuộc đường tròn \(\left( C \right)\) sao cho khoảng cách từ \(M\) đến \(A\left( 6;-10;3 \right)\) lớn nhất.
-
Có bao nhiêu số nguyên \(a\) để phương trình \({{z}^{2}}-\left( a-3 \right)z+{{a}^{2}}+a=0\) có hai nghiệm phức \({{z}_{1}}\), \({{z}_{2}}\)thỏa mãn \(\left| {{z}_{1}}+{{z}_{2}} \right|=\left| {{z}_{1}}-{{z}_{2}} \right|\)?
-
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu đạo hàm như hình vẽ
Hàm số đã cho có bao nhiêu điểm cực trị
-
Giả sử \(f\left( x \right)\) là hàm liên tục \(\left( 0;\,+\infty \right)\) và diện tích hình phẳng được kẻ sọc hình bên bằng \(3\). Tích phân \(\int\limits_{0}^{1}{f\left( 2x \right)\text{d}x}\) bằng
.PNG)
-
Cho các số phức \(z=2+i\) và \(w=3-i.\) Phần thực của số phức \(z+w\) bằng:
-
Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình bên. Hỏi phương trình \(2f\left( x \right)=5\) có bao nhiêu nghiệm trên đoạn \(\left[ -1;2 \right]\)?
-
Xét các số phức \(z=a+bi,\,\,\left( a,\,\,b\in \mathbb{R} \right)\) thỏa mãn \(\left| z-2+3i \right|=4\) và \(\left| z+1-4i \right|+\left| z-9 \right|\) đạt giá trị lớn nhất. Khi đó \(5a-2b\) bằng
-
Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào trong các khoảng dưới đây?
.png)
-
Xét tất cả các số thực dương \(x;y\) thỏa mãn \(\frac{x+y}{10}+\log \left( \frac{1}{2x}+\frac{1}{2y} \right)=1+2xy\). Khi biểu thức \(\frac{4}{{{x}^{2}}}+\frac{1}{{{y}^{2}}}\) đạt giá trị nhỏ nhất, tích \(xy\) bằng
