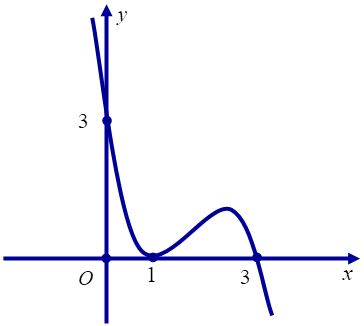
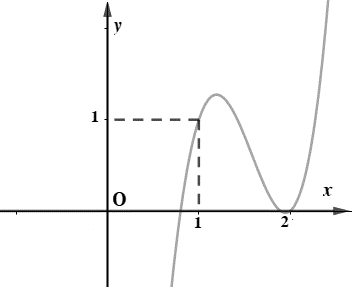
Cho hàm số bậc ba \(f(x)=a{{x}^{3}}+b{{x}^{2}}+cx+d\) có đồ thị như hình vẽ dưới đây

Số đường tiệm cận đứng của đồ thị hàm số \(g\left( x \right)=\frac{\left( {{x}^{2}}-3x+2 \right)\sqrt{x-1}}{\left( x+1 \right)\left[ {{f}^{2}}\left( x \right)-f\left( x \right) \right]}\)

A. \(5\).

B. \(3\).

C. \(6\).

D. \(4\).

Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án

Chủ đề: Đề thi THPT QG

Môn: Toán

Lời giải:

Báo sai

Nhận xét 1: Với \(x_{0}^{{}}\ge 1\) và \(\underset{x\to x_{0}^{+}}{\mathop{\lim }}\,g\left( x \right)\) hoặc \(\underset{x\to x_{0}^{-}}{\mathop{\lim }}\,g\left( x \right)\) có kết quả là \(+\infty \) hoặc \(-\infty \) thì \(x=x_{0}^{{}}\) là tiệm cận đứng của của đồ thị hàm số \(g\left( x \right)\).

Nhận xét 2: Dựa vào đồ thị hàm số \(f\left( x \right)\) ta có: \(f\left( x \right)=a\left( x-x_{1}^{{}} \right){{\left( x-2 \right)}^{2}}\).

Ta có

\( \left( x+1 \right)\left[ {{f}^{2}}\left( x \right)-f\left( x \right) \right]=0\\ \Leftrightarrow \left[ \begin{align} & x=-1 \\ & f\left( x \right)=0 \\ & f\left( x \right)=1 \\ \end{align} \right..\)

\(f\left( x \right)=0\Leftrightarrow \left[ \begin{align} & x=x_{1}^{{}}\,,\,0 < x_1 < 1 \\ &x=2. \end{align}\right.\)

\(f\left( x \right)=1\Leftrightarrow \left[ \begin{align} & x=1 \\ & x=x_{2}^{{}}\,,\,1 < x_2 < 2 \\& x=x_{3}^{{}}\,,\,x_{3}^{{}} > 2 \\ \end{align} \right.\) suy ra \(f\left( x \right)-1=a\left( x-1 \right)\left( x-x_{2}^{{}} \right)\left( x-x_{3}^{{}} \right)\).

Khi đó ta có \(g\left( x \right)=\frac{\left( {{x}^{2}}-3x+2 \right)\sqrt{x-1}}{\left( x+1 \right)\left[ {{f}^{2}}\left( x \right)-f\left( x \right) \right]}=\frac{\left( x-1 \right)\left( x-2 \right)\sqrt{x-1}}{\left( x+1 \right).f\left( x \right)\left[ f\left( x \right)-1 \right]}\).

\(g\left( x \right)=\frac{\left( x-1 \right)\left( x-2 \right)\sqrt{x-1}}{\left( x+1 \right).a\left( x-x_{1}^{{}} \right){{\left( x-2 \right)}^{2}}.a\left( x-1 \right)\left( x-x_{2}^{{}} \right)\left( x-x_{3}^{{}} \right)}=\frac{\sqrt{x-1}}{{{a}^{2}}\left( x+1 \right)\left( x-x_{1}^{{}} \right)\left( x-2 \right)\left( x-x_{2}^{{}} \right)\left( x-x_{3}^{{}} \right)}\).

\(x=-1\,,\,x=x_{1}^{{}}\) không phải tiệm cận đứng của đồ thị hàm số \(y=g\left( x \right)\) không thỏa mãn điều kiện \(x_{0}^{{}}\ge 1\). Đồ thị hàm số \(g\left( x \right)\) có \(3\) đường tiệm cận đứng là: \(x=2,\,x=x_{2}^{{}},\,x=x_{3}^{{}}\).

Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài