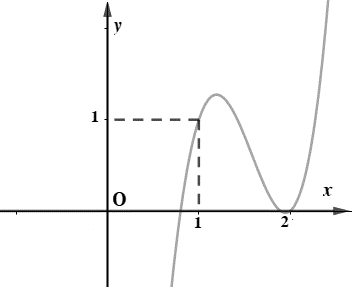
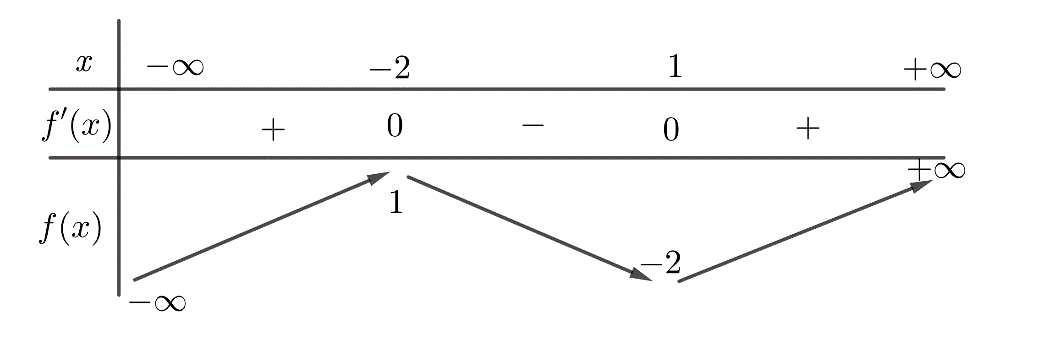
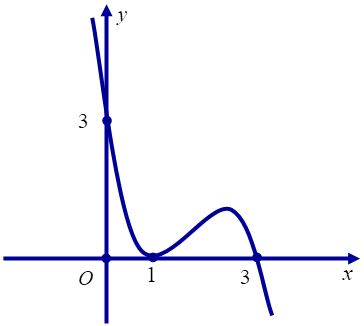
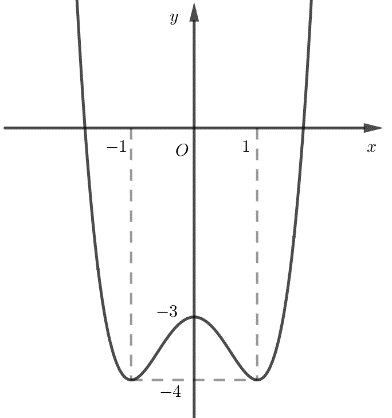
Cho hàm số đa thức bậc bốn \(y=f\left( x \right)\), đồ thị của hàm số \(y={f}'\left( 1-x \right)\) là đường cong ở hình vẽ.
Hàm số \(h\left( x \right)=f\left( x \right)-\frac{3}{2}{{x}^{2}}\) đạt giá trị nhỏ nhất trên \(\left[ 0;2 \right]\) tại
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiDo
\({f}'\left( 1-x \right)=0\Leftrightarrow \left[ \begin{align} & x=1 \\ & x=3 \\ \end{align} \right.\)
(với \(x=1\) là nghiệm kép);\(\underset{x\to +\infty }{\mathop{\lim }}\,{f}'\left( 1-x \right)=-\infty \) và \(y={f}'\left( 1-x \right)\) là hàm số bậc ba nên \({f}'\left( 1-x \right)=-k{{\left( x-1 \right)}^{2}}\left( x-3 \right)\) (với \(k>0\)).
\(\Rightarrow {f}'\left( 1-x \right)=k{{\left( 1-x \right)}^{2}}\left( 2+1-x \right)\).
\(\Rightarrow {f}'\left( x \right)=k{{x}^{2}}\left( 2+x \right)\).
Đồ thị của hàm số \(y={f}'\left( 1-x \right)\) đi qua điểm có tọa độ \(\left( 0;3 \right)\) nên \({f}'\left( 1-0 \right)=3\Leftrightarrow {f}'\left( 1 \right)=3\)
\(\Rightarrow k{{.1}^{2}}\left( 2+1 \right)=3\Leftrightarrow k=1\).
Khi đó \({f}'\left( x \right)={{x}^{2}}\left( 2+x \right)\).
Ta có \({h}'\left( x \right)={f}'\,\left( x \right)-3x={{x}^{2}}\left( 2+x \right)-3x=x\left( {{x}^{2}}+2x-3 \right)\).
Cho
\({h}'\left( x \right)=0\Leftrightarrow x\left( {{x}^{2}}+2x-3 \right)=0\\\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=1 \\ & x=-3 \\ \end{align} \right.\).
Bảng biến thiên
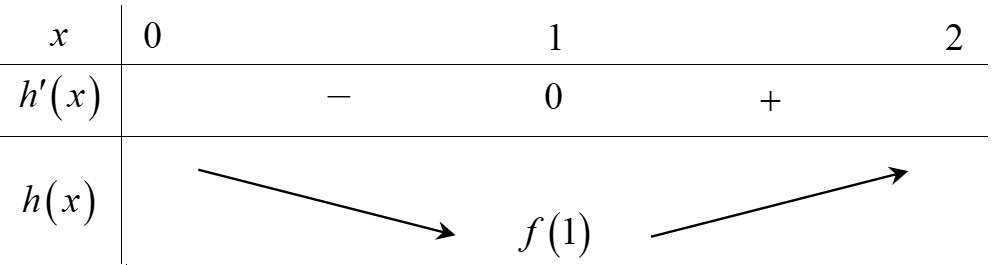
Khi đó hàm số \(h\left( x \right)=f\left( x \right)-\frac{3}{2}{{x}^{2}}\) đạt giá trị nhỏ nhất trên \(\left[ 0;2 \right]\) tại \(x=1\).
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Nguyễn Kiệm
Câu hỏi liên quan
-
Trong hình vẽ dưới đây, điểm \(M\) là điểm biểu diễn của số phức nào?
.png)
-
Tổng các nghiệm của phương trình \({{\log }_{\sqrt{2}}}\left( x-1 \right)+\log \left( x+3 \right)=1\) bằng
-
Cho khối chóp có diện tích đáy \(B=6\) và chiều cao \(h=2.\) Thể tích của khối chóp đã cho bằng
-
Một cấp số nhân gồm ba số hạng, biết số hạng thứ nhất và thứ hai lần lượt là \(-1;\,3.\) Số hạng cuối của cấp số nhân đó bằng
-
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ:
Số giá trị nguyên của tham số \(m\) để hàm số \(g\left( x \right)=f\left[ f\left( x \right)-m+1 \right]\) có đúng \(6\) điểm cực trị là
-
Cho hàm số bậc ba \(y=f\left( x \right)=m{{x}^{3}}+n{{x}^{2}}+\frac{1}{3}x+q\) có đồ thị \(\left( C \right)\) và cắt đường thẳng \(d:y=g\left( x \right)\) như hình vẽ. Biết \(AB=5\), tổng tất cả các nghiệm của phương trình \(f\left( x \right)-g\left( x \right)-3{{x}^{2}}=2\) là
-
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
-
Cho phương trình\({{z}^{2}}+az+2{{a}^{2}}=0\), với \(a\) là số thực dương. Gọi \({{z}_{1}},{{z}_{2}}\) là hai nghiệm phức của phương trình, trong đó \({{z}_{1}}\)có phần ảo dương. Biết rằng \(\left( 2{{z}_{1}}+{{z}_{2}} \right)\overline{{{z}_{1}}}=10+2\sqrt{7}i\). Khẳng định làm sau đây đúng?
-
Số phức liên hợp của số phức \(z=-2+3i\) là
-
Cho hai số phức \({{z}_{1}},\,\,{{z}_{2}}\) thỏa mãn \(\left| {{z}_{1}}+2-i \right|+\left| {{z}_{1}}-4-7i \right|=6\sqrt{2}\) và \(\left| i{{z}_{2}}-1+2i \right|=1.\) Giá trị nhỏ nhất của biểu thức \(P=\left| {{z}_{1}}+{{z}_{2}} \right|\) bằng
-
Lấy ngẫu nhiên một số tự nhiên nhỏ hơn \(100,\) xác suất để lấy được một số chia hết cho \(6\) bằng
-
Cho \(g\left( x \right)={{x}^{2}}-2x-1\) và hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ:
Số nghiệm của phương trình \(f\left[ g\left( x \right) \right]=0\) là
-
Đồ thị hàm số \(y=\frac{x-4}{2x+2}\) cắt trục tung tại điểm có tung độ bằng
-
Cho hình hộp đứng có đáy là hình vuông cạnh bằng \(a,\) độ dài cạnh bên bằng \(3a.\) Thể tích của khối hộp đã cho bằng
-
Trong không gian \(Oxyz,\) cho mặt phẳng \(\left( P \right):x-y+z+7=0,\) đường thẳng \(d:\frac{x}{1}=\frac{y}{-2}=\frac{z}{2}\) và mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z-2 \right)}^{2}}=5.\) Gọi \(A,\,\,B\) là hai điểm trên mặt cầu \(\left( S \right)\) và \(AB=4;\) \({A}',\,\,{B}'\) là hai điểm nằm trên mặt phẳng \(\left( P \right)\) sao cho \(A{A}',\,\,B{B}'\) cùng song song với đường thẳng \(d.\) Giá trị lớn nhất của tổng \(A{A}'+\,B{B}'\) gần nhất với giá trị nào sau đây
-
Đạo hàm của hàm số \(y={{5}^{2x}}\) là
-
Tập nghiệm của bất phương trình \({{\log }_{3}}\left( x-2 \right)\le 2\) là
-
Cho mặt cầu có đường kính bằng \(8.\) Diện tích của mặt cầu đã cho bằng
-
Tiệm cận đứng của đồ thị hàm số \(y=\frac{2x-1}{x+1}\) là đường thẳng có phương trình
-
Cho hàm số \(y=f\left( x \right)\), hàm số \(y={f}'\left( x \right)\) liên tục trên \(R\) và có đồ thị như hình vẽ.
Bất phương trình \(f\left( x \right)-{{\left( x-1 \right)}^{3}}>m+5x+1\) (với \(m\) là tham số thực) nghiệm đúng với mọi \(x\in \left( 0\,;\,3 \right)\) khi và chỉ khi
