Trắc nghiệm Hàm số lũy thừa Toán Lớp 12
-
Câu 1:
Tập nghiệm của bất phương trình log34x+6x≤0log34x+6x≤0 là:
A. S=[−2;−32)S=[−2;−32)
B. S=[−2;0)S=[−2;0)
C. S=(−∞;2]S=(−∞;2]
D. S=R∖[−32;0]S=R∖[−32;0]
-
Câu 2:
Tập nghiệm của bất phương trình log12(x−1)≥0log12(x−1)≥0 là:
A. (1;2)
B. (1;2]
C. (−∞;2](−∞;2]
D. [2;+∞)[2;+∞)
-
Câu 3:
Tìm tập nghiệm của bất phương trình log12(x2−3x+2)≥−1log12(x2−3x+2)≥−1
A. (−∞;1)(−∞;1)
B. [0;1)∪(2;3][0;1)∪(2;3]
C. [0;2)∪(3;7][0;2)∪(3;7]
D. [0;2)[0;2)
-
Câu 4:
Tìm tập nghiệm S của bất phương trình log122x−1>2log122x−1>2
A. S=(1;1+√2)S=(1;1+√2)
B. S=(1;9)S=(1;9)
C. S=(1+√2;+∞)S=(1+√2;+∞)
D. S=(9;+∞)S=(9;+∞)
-
Câu 5:
Tập nghiệm của bất phương trình log12x2≥−1log12x2≥−1 là
A. [√2;+∞).[√2;+∞).
B. [−√2;0)∪(0;√2].[−√2;0)∪(0;√2].
C. [−√2;√2].[−√2;√2].
D. (0;√2].(0;√2].
-
Câu 6:
Tìm tập nghiệm của bất phương trình log0,5(2x−1)>−2log0,5(2x−1)>−2
A. S=(12;52)S=(12;52)
B. S=[12;52)S=[12;52)
C. S=(−∞;52)S=(−∞;52)
D. S=(52;+∞)S=(52;+∞)
-
Câu 7:
Tập nghiệm của bất phương trình 3<log2x<43<log2x<4 là:
A. (8;16)
B. (0;16)
C. (8;+∞)(8;+∞)
D. R
-
Câu 8:
Giải bất phương trình log34(2x−1)>2log34(2x−1)>2 ta được:
A. 12<x<2532
B. x>2532
C. x<12 hoặc x>2532
D. x>12
-
Câu 9:
Tập nghiệm của bất phương trình log12(2x−1)>−1 là:
A.
(1;32)
B. (32;+∞)
C. (12;32)
D. (−∞;32)
-
Câu 10:
Bất phương trình log2(x2−2x+3)>1 có tập nghiệm là
A. R \ {1}
B. R
C. {1}
D. ∅
-
Câu 11:
Tìm tọa độ giao điểm M của hai đồ thị hàm số y=3x và y=13.
A. M(−1;−13)
B. M(−1;13)
C. M(1;13)
D. M(1;−13)
-
Câu 12:
Đường cong ở hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?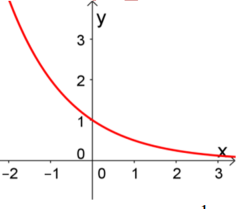
A. y=−x2+2x+1
B. y=log0,5x
C. y=12x
D. y=2x
-
Câu 13:
Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở
bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?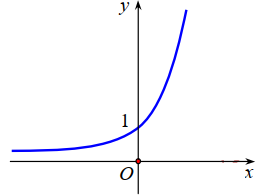
A. y=(12)x
B. y=x2
C. y=log2x
D. y=2x
-
Câu 14:
Hàm số nào trong các hàm số dưới đây có đồ thị phù hợp với hình vẽ bên?
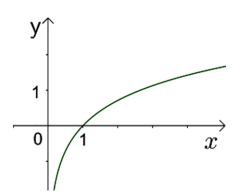
A. y=log0,5x
B. y=log√7x
C. y=ex
D. y=e−x
-
Câu 15:
Cho α,β là các số thực. Đồ thị các hàm số y=xα,y=xβtrên khoảng (0;+∞) được cho trong hình vẽ bên. Khẳng định nào sau đây là đúng?
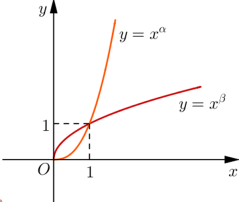
A. 0<β<1<α
B. β<0<1<α
C. 0<α<1<β
D. α<0<1<β
-
Câu 16:
Cho hàm số y=x−√2 . Mệnh đề nào sau đây là sai?
A. Đồ thị hàm số không cắt trục hoành
B. Hàm số nghịch biến trên (0;+∞)
C. Hàm số có tập xác định là (0;+∞)
D. Đồ thị hàm số không có tiệm cận
-
Câu 17:
Cho hàm số y=xe−3trong các kết luận sau kết luận nào sai?
A. Đồ thị hàm số nhận Ox, Oy làm hai tiệm cận.
B. Đồ thị hàm số luôn đi qua M(1;1)
C. Hàm số luôn đồng biến trên (0;+∞)
D. Tập xác định của hàm số là D=(0;+∞)
-
Câu 18:
Cho hàm số y=x−√2017 . Mệnh đề nào dưới đây là đúng về đường tiệm cận của đồ thị hàm số
A. Có một tiệm cận ngang và một tiệm cận đứng.
B. Không có tiệm cận ngang và có một tiệm cận đứng.
C. Có một tiệm cận ngang và không có tiệm cận đứng.
D. Không có tiệm cận
-
Câu 19:
Hình vẽ bên là đồ thị các hàm số y=xa,y=xb,y=xc trên miền (0;+∞) . Hỏi trong các số a, b, c số nào nhận giá trị trong khoảng (0; 1) ?
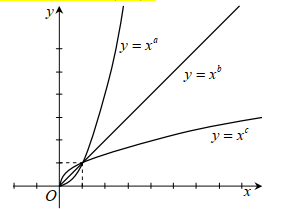
A. Số a
B. Số a và số c
C. Số b
D. Số c
-
Câu 20:
Hàm số nào trong hàm số sau đây có đồ thị phù hợp với hình vẽ bên
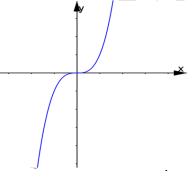
A. y=x3
B. y=x4
C. y=x15
D. y=√x
-
Câu 21:
Tính đạo hàm của hàm số y=log(ln2x)
A. y′=2xln2x.ln10
B. y′=1xln2x.ln10
C. y′=12xln2x.ln10
D. y′=1xln2x
-
Câu 22:
Cho hàm số f(x)=ln(x⁴+1) . Đạo hàm f'(1) bằng
A. ln22
B. 1
C. 12
D. 2
-
Câu 23:
Đạo hàm của hàm số y=log3(x+1)−2ln(x−1)+2x tại điểm x = 2 bằng
A. 13
B. 13ln3+2
C. 13ln3−1
D. 13ln3
-
Câu 24:
Cho hàm số y=2xex+3sin2x .Khi đó y'(0) có giá trị bằng
A. 8
B. -4
C. 2
D. 5
-
Câu 25:
Đạo hàm của hàm số y=log(2sinx−1) trên tập xác định là:
A. y′=−2cosx2sinx−1
B. y′=2cosx2sinx−1
C. y′=2cosx(2sinx−1)ln10
D. y′=−2cosx(2sinx−1)ln10
-
Câu 26:
Đạo hàm của hàm số y=log8(x²−3x−4) là
A. 2x−3(x2−3x−4)ln8
B. 2x−3(x2−3x−4)ln2
C. 2x−3(x2−3x−4)
D. 1(x2−3x−4)ln8
-
Câu 27:
Cho hàm số f(x)=ln(4x−x²). Chọn khẳng định đúng?
A. f'(3)=-1,5
B. f'(2)=0
C. f'(5)=1,2
D. f'(-1)=-1,2
-
Câu 28:
Tính đạo hàm của hàm số y=log2017(x+1)
A. y′=2x2017
B. y′=2x(x2+1)ln2017
C. y′=1(x2+1)ln2017
D. y′=1(x2+1)
-
Câu 29:
Đạo hàm của hàm số y=log3(4x+1) là
A. y′=1(4x+1)ln3
B. y′=4(4x+1)ln3
C. y′=ln3(4x+1)
D. y′=4ln34x+1
-
Câu 30:
Tính đạo hàm của hàm số y=√x3√x4√x
A. y′=7.24√x724
B. y′=14.24√x724
C. y′=1724.24√x7
D. y′=724.24√x7
-
Câu 31:
Cho hàm số y=xπ . Tính y''(1).
A. y″(1)=ln2π
B. y″(1)=πlnπ
C. y″(1)=0
D. y″(1)=π(π−1)
-
Câu 32:
Đạo hàm của hàm số y=(5x2−x+2)13
A. y′=10x−13.3√5x2−x+2
B. y′=10x−13√(5x2−x+2)2
C. y′=10x−13.3√(5x2−x+2)2
D. y′=13.3√5x2−x+2
-
Câu 33:
Hàm số y=loga2−2a+1x nghịch biến trong khoảng (0;+∞) khi
A. a≠1và0<a<2
B. a>1
C. a<0
D. a≠1vàa>12
-
Câu 34:
Hàm số y=log2(x3−4x) có bao nhiêu điểm cực trị?
A. 0
B. 2
C. 1
D. 2
-
Câu 35:
Hàm số y=log0,5(−x²+2x) đồng biến trên khoảng nào sau đây?
A. (−∞;1)
B. (0;1)
C. (1;+∞)
D. (1;2)
-
Câu 36:
Hàm số y=ln(x+2)+3x+2 đồng biến trên khoảng nào ?
A. (−∞;1)
B. (1;+∞)
C. (12;1)
D. (−12;+∞)
-
Câu 37:
Đồ thị hàm số y=lnxxcó tọa độ điểm cực đại là (a;b). Khi đó ab bằng
A. e
B. 2e
C. 1
D. -1
-
Câu 38:
Hàm số log2(x3−4x) có bao nhiêu điểm cực trị?
A. 0
B. 2
C. 1
D. 3
-
Câu 39:
Trong các hàm số sau, hàm số nào nghịch biến trong khoảng (0;+∞)
A. y=log2x
B. y=x2+log2x
C. y=x+log2x
D. y=log21x
-
Câu 40:
Hàm số nào dưới đây đồng biến trên R
A. y=(π4)x
B. y=1(√7−√5)x
C. y=15x
D. y=(e3)x
-
Câu 41:
Trong các hàm số sau, hàm số nào nghịch biến trên khoảng (0;+∞)
A. y=x+log2x
B. y=x+log21x
C. y=x2+log2x
D. y=−log2x
-
Câu 42:
Trong các hàm số sau, hàm số nào đồng biến trên R
A. y=(π4)x
B. y=(2e)x
C. y=(2√3+1)x
D. y=(e+1π)x
-
Câu 43:
Cho hàm số y=14x Mệnh đề nào sau đây là mệnh đề SAI?
A. Hàm số đã cho đồng biến trên khoảng (−∞;+∞)
B. Hàm số đã cho nghịch biến trên khoảng (−∞;0)
C. Hàm số đã cho nghịch biến trên khoảng (−∞;+∞)
D. Hàm số đã cho nghịch biến trên khoảng (0;+∞)
-
Câu 44:
Hàm số nào dưới đây đồng biến trên tập xác định của nó?
A. y=(1π)x
B. y=(23)x
C. y=(√3)x
D. y=(0,5)x
-
Câu 45:
Cho hàm số y=(34)x2−2x+2 . Trong các khẳng định dưới đây, khẳng định nào đúng?
A. Hàm số luôn đồng biến trên R
B. Hàm số luôn nghịch biến trên khoảng (−∞;1)
C. Hàm số luôn đồng biến trên trên (−∞;1)
D. Hàm số luôn nghịch biến trên R
-
Câu 46:
Hàm số nào sau đây nghịch biến trên tập xác định của nó?
A. y=logeπx
B. y=log√3x
C. y=lg2x
D. y=logπx
-
Câu 47:
Hàm số nào sau đây đồng biến trên tập xác định của nó?
A. y=log2(1−x)
B. y=20172−x
C. y=log12(3−x)
D. y=(√32)x+1
-
Câu 48:
Đồ thị hàm số nào sau đây đối xứng với đồ thị hàm số y=10−xqua đường thẳng y = x .
A. y=logx
B. y=lnx
C. y=−logx
D. y=10x
-
Câu 49:
Cho hàm số y=log2x . Mệnh đề nào dưới đây sai?
A. Đạo hàm của hàm số là y′=1xln2
B. Đồ thị hàm số nhận trục Oy làm tiệm cận đứng.
C. Tập xác định của hàm số là (−∞;+∞)
D. Hàm số đồng biến trên khoảng (0;+∞)
-
Câu 50:
Cho hàm số y=log√3x . Mệnh đề nào dưới đây là mệnh đề sai?
A. Hàm số đã cho đồng biến trên tập xác định.
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có một tiệm cận đứng là trục Oy
D. Hàm số đã cho có tập xác định D=R∖{0}














