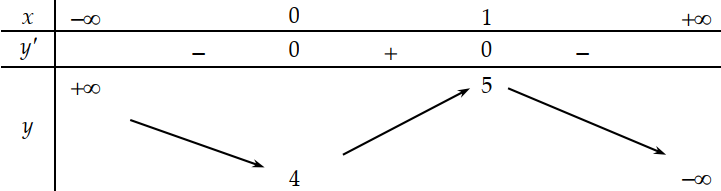Trắc nghiệm Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán Lớp 12
-
Câu 1:
Tìm giá trị nhỏ nhất của hàm số \(y=\sin ^{2} x-4 \sin x-5\)?
A. -2
B. -4
C. -6
D. -8
-
Câu 2:
Hàm số y\(y=x+\frac{10^{8}}{x}\) đạt giá trị nhỏ nhất trên đoạn \(\left[10^{3} ; 10^{9}\right] \) tại x bằng:
A. \(10^{2}\)
B. \(10^{3}\)
C. \(10^{4}\)
D. \(10^{5}\)
-
Câu 3:
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y=\sqrt{x-1}+\sqrt{7-x} .\) . Khi đó
có bao nhiêu số nguyên dương nằm giữa m và M ?A. 1
B. 2
C. 3
D. 4
-
Câu 4:
Tìm giá trị lớn nhất của hàm số \(y=f(x)=\sqrt{x-1}+\sqrt{5-x}\) trên đoạn [1;5]
A. \(\max \limits_{[1 ; 5]} f(x)=2 \sqrt{2}-1 .\)
B. \(\max \limits _{[1 ; 5]} f(x)=\sqrt{2}-1 .\)
C. \(\max \limits _{[1 ; 5]} f(x)=2 \sqrt{2} . \)
D. \(\max \limits _{[1 ; 5]} f(x)=2 .\)
-
Câu 5:
Tìm giá trị nhỏ nhất của hàm số \(y=x+\frac{9}{x}\) trên đoạn \([2 ; 4] .\)
A. \(\frac{13}{2}\)
B. \(\frac{27}{2}\)
C. 6
D. -3
-
Câu 6:
Tìm giá trị nhỏ nhất của hàm số \(y=\frac{x^{2}+3}{x-1}\) trên đoạn [2 ; 4] .
A. -2
B. -3
C. 4
D. 6
-
Câu 7:
Giá trị nhỏ nhất của hàm số \(f(x)=x+\frac{1}{x}\) trên nửa khoảng \([2 ;+\infty)\) là?
A. 2
B. 1
C. \(\frac{5}{2}\)
D. \(\frac{7}{2}\)
-
Câu 8:
Giá trị lớn nhất của hàm số \(f(x)=\frac{x}{x+3}\) trên đoạn [-2; 3] bằng
A. 2
B. 3
C. \(\frac{1}{2}\)
D. 1
-
Câu 9:
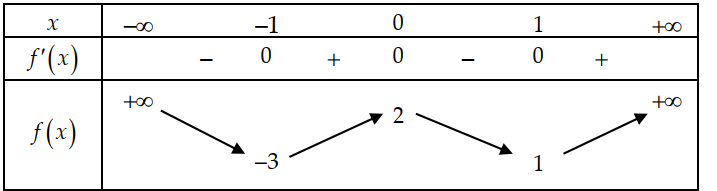
Cho hàm số y=f(x) có bảng biến thiên như sau:
.PNG)
\(\text { Đặt } g(x)=[f(x)]^{3}-3[f(x)]^{2}\).Khẳng định nào sau đây đúng?
A. \(\max\limits _{[-1 ; 1]} g(x)=-4 . \)
B. \(\max\limits _{[-1 ; 1]} g(x)=4 .\)
C. \(\max\limits _{[-1 ; 1]} g(x)=0 .\)
D. \(\max\limits _{[-1 ; 1]} g(x)=2\)
-
Câu 10:
Cho hàm số y=f(x) có bảng biến thiên như sau:
.PNG)
\(\begin{equation} \text { Đặt } g(x)=f(\cos x) \text { . } \end{equation}\)Khẳng định nào sau đây đúng?
A. \(\min\limits _{\left[0 ; \frac{\pi}{2}\right]} g(x)=1 .\)
B. \(\min\limits _{\left[0 ; \frac{\pi}{2}\right]} g(x)=2 \)
C. \(\min\limits _{\left[0 ; \frac{\pi}{2}\right]} g(x)=-3 .\)
D. \(\min\limits _{\left[0 ; \frac{\pi}{2}\right]} g(x)=0\)
-
Câu 11:
Cho hàm số y=f(x) có bảng biến thiên như sau:
\(\begin{equation} \text { Đặt } g(x)=f(\sin x) \text { . } \end{equation}\)Khẳng định nào sau đây đúng?
A. \(\begin{equation} \max\limits _{\mathbb{R}} g(x)=2 . \end{equation}\)
B. \(\max \limits _{\mathbb{R}} g(x)=1 .\)
C. \(\max\limits _{\mathbb{R}} g(x)=3 .\)
D. \( \max\limits _{\mathbb{R}} g(x)=4 .\)
-
Câu 12:
Cho hàm số y =f(x) có bảng biến thiên như sau:
.PNG)
Khẳng định nào sau đây đúng?
A. \(\begin{equation} \max\limits _{x \in[-1 ; 1]}|f(x)|=2 . \end{equation}\)
B. \( \max\limits_{x \in[-1 ; 1]}|f(x)|=1 .\)
C. \(\max\limits _{x \in[-1 ; 1]}|f(x)|=0 .\)
D. \( \max\limits _{x \in[-1 ; 1]}|f(x)|=3 .\)
-
Câu 13:
Cho hàm số y=f(x) có bảng biến thiên như sau:
.PNG)
\(\begin{equation} \text { Đặt } g(x)=3-4 f(x) \text { . } \end{equation}\)Khẳng định nào sau đây đúng?
A. \(\begin{equation} \min\limits _{x \in[-1 ; 1]} g(x)=15 . \end{equation}\)
B. \(\min\limits _{x \in[-1 ; 1]} g(x)=-5 .\)
C. \(\min\limits _{x \in[-1 ; i]} g(x)=-15 .\)
D. \(\max \limits _{x \in[-1 ; 1]} g(x)=-3 .\)
-
Câu 14:
Cho hàm số \(\begin{equation} y=f(x) \end{equation}\) có bảng biến thiên như sau:
.PNG)
\(\begin{equation} \text { Đặt } g(x)=2 f(x)+1 \end{equation}\). Khẳng định nào sau đây đúng?
A. \(\begin{equation} \max \limits_{x \in[-1 ; 1]} g(x)=2 . \end{equation}\)
B. \(\max\limits _{x \in[-1 ; 1]} g(x)=5 .\)
C. \( \max \limits_{x \in[-1 ; 1]} g(x)=1 \)
D. \(\max \limits_{x \in[-1 ; 1]} g(x)=-5 .\)
-
Câu 15:
Cho hàm số \(\begin{equation} y=f(x) \end{equation}\) có bảng biến thiên như sau:
.PNG)
Khẳng định nào sau đây đúng?
A. \(\begin{equation} \max\limits _{x \in[-15 ;-5]} f(x)=f(-5) . \end{equation}\)
B. \(\max \limits _{x \in[-15 ;-5]} f(x)=f(-15) \)
C. \(\max\limits _{x \in[-15 ;-5]} f(x)=2\)
D. \(\max \limits _{x \in[-15 ;-5]} f(x)=f(-10) \text { . }\)
-
Câu 16:
Cho hàm số y =f(x) có bảng biến thiên như sau:
.PNG)
Khẳng định nào sau đây đúng?
A. \(\begin{equation} \max \limits_{x[5 ; 15]} f(x)=f(5) . \end{equation}\)
B. \( \max \limits _{x \in[5 ; 15]} f(x)=f(15) .\)
C. \( \max \limits_{x \in[5 ; 15]} f(x)=2 .\)
D. \( \max \limits _{x[[5 ; 15]} f(x)=f(10) .\)
-
Câu 17:
Cho hàm số y=f(x) có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A. \(\begin{equation} \begin{array}{l} \max\limits _{x \in[-1 ; 1]} f(x)=2 . \end{array} \end{equation}\)
B. \(\max\limits _{x \in[-1 ; 1]} f(x)=1 .\)
C. \( \max \limits_{x \in[-1 ; 1]} f(x)=0 .\)
D. \( \max\limits _{x \in[-1 ; 1]} f(x)=-3\)
-
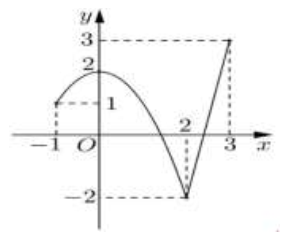
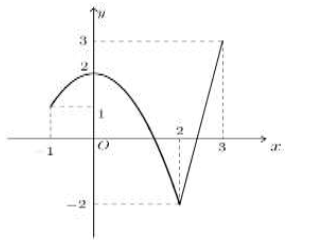
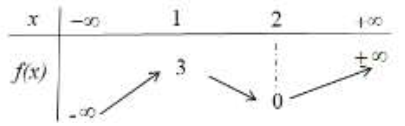
Câu 18:
Cho hàm số \(\begin{equation} y=f(x) \end{equation}\) liên tục trên đoạn (-1;3) và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn [-1;3] . Giá trị của M-m bằng
A. 2
B. 3
C. 4
D. 5
-
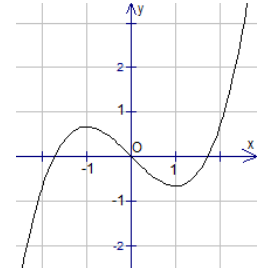
Câu 19:
Cho hàm số y=f(x) có đạo hàm cấp 2 trên , hàm số \(y=f^{\prime}(x)\) có đồ thị như hình vẽ bên
Giá trị lớn nhất của hàm số \(y=f\left(\frac{\sin x+\sqrt{3} \cos x}{2}\right) \text { trên đoạn }\left[-\frac{5 \pi}{6} ; \frac{\pi}{6}\right]\) bằng:
A. \(f\left(-\frac{5 \pi}{6}\right) .\)
B. \(f\left(-\frac{\pi}{3}\right)\)
C. \(f(0) .\)
D. \(f\left(\frac{\pi}{6}\right)\)
-
Câu 20:
Cho hàm số y=f(x) có đồ thị như hình dưới. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y=f(-2 x) \text { trên }\left[-1 ; \frac{1}{2}\right]\) Giá trị m+M bằng
A. -2
B. 3
C. -4
D. 5
-
Câu 21:
Cho hàm số f(x) lên tục trên đoạn [-1; 3] và có đồ thị như hình vẽ bên. Giá trị lớn nhất của hàm số \(y=f\left(3 \sin ^{2} x-1\right)\) bằng
A. 0
B. 1
C. 2
D. 3
-
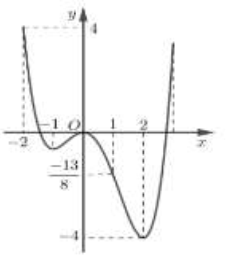
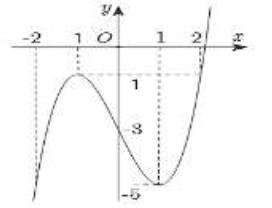
Câu 22:
Cho hàm số y=f(x) xác định và liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y=f(x) trên đoạn [-2;2]?
A. \(m=-5 ; M=-1 .\)
B. \(m=-2 ; M=2 . \)
C. \(m=-1 ; M=0 .\)
D. \(m=-5 ; M=0 .\)
-
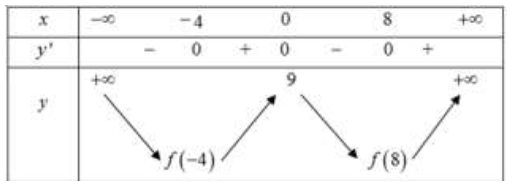
Câu 23:
Hàm số y=f(x) liên tục trên và có bảng biến thiên như hình bên dưới
Biết f(-4)>f(8), khi đó giá trị nhỏ nhất của hàm số đã cho trên R bằng
A. 9
B. f(-4)
C. f(8)
D. 4
-
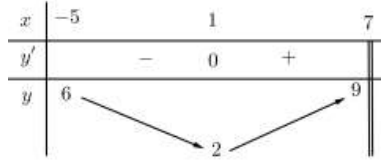
Câu 24:
Cho hàm số y=f(x ) có bảng biến thiên trên \([-5 ; 7)\) như sau:
Mệnh đề nào dưới đây đúng?
A. \(\min\limits _{[-5 ; 7)} f(x)=6 .\)
B. \( \min \limits_{[-5 ; 7)} f(x)=2 .\)
C. \(\max\limits _{[-5 ; 7)} f(x)=9 .\)
D. \( \max \limits_{[-5 ; 7)} f(x)=6 .\)
-
Câu 25:
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên. Mệnh đề nào dưới đây đúng ?
A. \(y_{C Đ}=5\)
B. \(y_{C T}=0\)
C. \(\min\limits _{\mathbb{R}} y=4\)
D. \(\max\limits _{\mathbb{R}} y=5\)
-
Câu 26:
Cho hàm số y=f(x) xác định, liên tục trên và có bảng biến thiên như sau:
Giá trị lớn nhất của hàm số y=f(x) trên đoạn [ 0; 2] bằng:
A. 0
B. 1
C. 2
D. 3
-
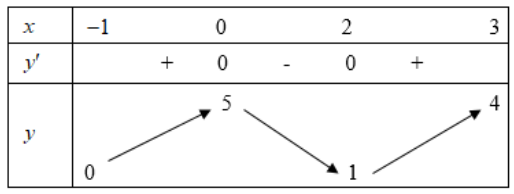
Câu 27:
Cho hàm số y =f(x)liên tục và có bảng biến thiên trên đoạn [-1; 3] như hình vẽ. Khẳng định nào sau đây đúng?
A. \(\max\limits _{[-1 ; 3]} f(x)=f(0) \)
B. \(\max \limits_{[-1 ; 3]} f(x)=f(3) .\)
C. \(\max\limits _{[-1 ; 3]} f(x)=f(2) .\)
D. \( \max\limits _{[-1 ; 3]} f(x)=f(-1) .\)
-
Câu 28:
Cho hàm số \(y=\left|x^{3}-3 x^{2}+m\right|\)(với m là tham số thực). Hỏi \(\max _{[1 ; 2]} y\) có giá trị nhỏ nhất bằng bao nhiêu?
A. 2
B. 3
C. 4
D. 1
-
Câu 29:
Xét hàm số \(\begin{equation} f(x)=\left|x^{2}+a x+b\right| \end{equation}\) , với a , b là tham số. Gọi M là giá trị lớn nhất của hàm số
trên [-1;3]. Khi M nhận giá trị nhỏ nhất tính \(\begin{equation} T=a+2 b \text { . } \end{equation}\)A. -1
B. -2
C. -3
D. -4
-
Câu 30:
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số \(\begin{equation} y=\left|\frac{x^{2}+m x+m}{x+1}\right| \end{equation}\) trên [1;2] bằng 2 . Số phần tử của S là
A. 1
B. 2
C. 3
D. 4
-
Câu 31:
Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số \(\begin{equation} y=\left|\frac{x-m^{2}-m}{x+2}\right| \end{equation}\) thỏa \(\begin{equation} \max _{[1 ; 2]} y=1 \end{equation}\). Tích các phần tử của S bằng
A. -2
B. 4
C. -4
D. 2
-
Câu 32:
Gọi M là giá trị lớn nhất của hàm số \(\begin{equation} f(x)=\left|3 x^{4}-4 x^{3}-12 x^{2}+m\right| \end{equation}\) trên đoạn [-1;3]. Có bao nhiêu số thực m để \(\begin{equation} M=\frac{59}{2} ? \end{equation}\)
A. 1
B. 2
C. 4
D. 6
-
Câu 33:
Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số \(y=\left|x^{2}+x+m\right|\) thỏa mãn \(\min\limits _{[-2 ; 2]} y=2\) . Tổng tất cả các phần tử của S bằng
A. \(-\frac{23}{4}\)
B. \(-\frac{31}{4}\)
C. \(\frac{31}{4}\)
D. 0
-
Câu 34:
Gọi tập S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số \(y=\left|x^{3}-3 x+m\right|\) trên đoạn [0;2] bằng 3. Số phần tử của S là
A. 0
B. 1
C. 2
D. 6
-
Câu 35:
Một người nông dân có 15 000 000 đồng để làm một cái hàng rào hình chữ E dọc theo một con sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là 60 000 đồng là một mét, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là 50 000 đồng một mét. Tìm diện tích lớn nhất của đất rào thu được.
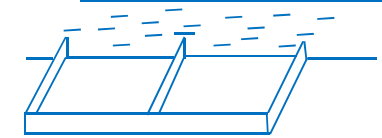
A. \(6250 \mathrm{m}^{2}\)
B. \(1250 \mathrm{m}^{2}\)
C. \(3125 m^{2}\)
D. \(50 \mathrm{m}^{2}\)
-
Câu 36:
Trong 1 cuộc thi pha chế, mỗi đội được dùng tối đa 24g hương liệu, 9 lít nước và 210g đường để pha nước cam và nước táo. Pha 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu; pha 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu. Mỗi lít nước cam được 60 điểm, mỗi lít nước táo được 80 điểm. Cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt điểm cao nhấ
A. 6 lít nước cam và 3 lít nước táo
B. 4 lít nước cam và 5 lít nước táo
C. 7 lít nước cam và 2 lít nước táo
D. 5 lít nước cam và 4 lít nước táo
-
Câu 37:
Một người đàn ông muốn chèo thuyền ở vị trí A tới điểm B về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng 3km (như hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua sông để đến C và sau đó chạy đến B, hay có thể chèo trực tiếp đến B, hoặc anh ta có thể chèo thuyền đến một điểm D giữa C và B và sau đó chạy đến B. Biết anh ấy có thể chèo thuyền 6 km/h , chạy 8 km/h và quãng đường BC = 8(km) . Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Tìm khoảng thời gian ngắn nhất (đơn vị: giờ) để người đàn ông đến B.
A. \(\frac{3}{2}\)
B. \(\frac{9}{\sqrt{7}}\)
C. \(\frac{\sqrt{73}}{6}\)
D. \(1+\frac{\sqrt{7}}{8}\)
-
Câu 38:
Hàm số \(y=\sqrt{x}+\frac{\sqrt{x}}{\sqrt{x}+1}\) có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [ 0; 4] lần lượt là:
A. \(\frac{8}{3} ; 0\)
B. \(\frac{8}{3} ;-\frac{8}{3}\)
C. \(0 ;-\frac{8}{3}\)
D. \(\frac{24}{5} ; 0\)
-
Câu 39:
Hàm số \(y=x^{2}+3 x+\sqrt{x^{2}+3 x+2}\) có giá trị nhỏ nhất bằng
A. -2
B. 0
C. 2
D. \(\sqrt2 \)
-
Câu 40:
Hàm số \(y=x^{8}+\left(x^{4}-1\right)^{2}\) đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [1; 2] lần lượt tại hai điểm có hoành độ \(x_{1} ; x_{2}\). Khi đó tích\(x_{1} . x_{2}\) có giá trị bằng
A. 1
B. 2
C. 15
D. 10
-
Câu 41:
Hàm số \(y=x+\frac{1}{x}+x^{2}+\frac{1}{x^{2}}\) có giá trị nhỏ nhất, giá trị lớn nhất trên đoạn [ 1; 3] là:
A. \(3 ; \frac{112}{9}\)
B. \(1 ; 4\)
C. \(4 ; \frac{112}{9}\)
D. \(4 ; \frac{112}{9}\)
-
Câu 42:
Hàm số \(y=\frac{\sin x+1}{\sin ^{2} x+3}\) đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn \(\left[-\frac{\pi}{2} ; \frac{\pi}{2}\right]\) tại điểm có hoành độ bằng
A. \(x=-\frac{\pi}{2} ; x=\frac{\pi}{2}\)
B. \(x=\frac{\pi}{6} ; x=\frac{\pi}{2}\)
C. \(x=\frac{\pi}{6} ; x=-\frac{\pi}{2}\)
D. \(x=0 ; x=\frac{\pi}{2}\)
-
Câu 43:
Hàm số \(y=\sqrt{x+1}+\sqrt[3]{x+1}\) có giá trị nhỏ nhất, giá trị lớn nhất trên đoạn [0; 63] là:
A. 2 ; 12
B. 1 ; 2
C. 0 ; 2
D. 0 ; 12
-
Câu 44:
Hàm số \(y=\sqrt{x+2}+\sqrt{2-x}+2 \sqrt{4-x^{2}}\) đạt giá trị lớn nhất, giá trị nhỏ nhất tại điểm có hoành độ là:
A. \(2 \sqrt{2}+4 ; 2\)
B. \(2 \sqrt{2}-2 ; 2\)
C. \(2 \sqrt{2} ; 2\)
D. \(4 ; 2\)
-
Câu 45:
Hàm số \(y=\sqrt{1-x}+\sqrt{x+3}+\sqrt{1-x} \cdot \sqrt{x+3}\) có giá trị lớn nhất, giá trị nhỏ nhất là:
A. \(2 \sqrt{2}-2 ; 2\)
B. \(2 \sqrt{2}+2 ; 2\)
C. \(2 \sqrt{2} ; 2\)
D. \(2 ; 0\)
-
Câu 46:
Hàm số \(y=(x-1)(x-2)(x-3)(x-4)\) có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [-1; 3] là:
A. \(10 ;-\frac{9}{4}\)
B. \(120 ; 1\)
C. \(10 ;-1\)
D. \(120 ;-1\)
-
Câu 47:
Hàm số \(y=\frac{x^{2}-2}{\sqrt{x^{2}+1}}\) có giá trị nhỏ nhất tại điểm có hoành độ bằng:
A. 0
B. 2
C. 3
D. 1
-
Câu 48:
Hàm số \(y=\left(x^{2}+2 x+3\right)\left(x^{2}+2 x-2\right)\) có giá trị lớn nhất là:
A. có giá trị lớn nhất là 0 .
B. có giá trị lớn nhất là -8.
C. có giá trị lớn nhất là 2
D. không có giá trị lớn nhất.
-
Câu 49:
Hàm số \(y=\sqrt{1+2 \sin x \cdot \cos x}\) đạt giá trị nhỏ nhất trên đoạn \(\left[0 ; \frac{\pi}{2}\right]\) tại điểm có hoành độ là:
A. \(x=\frac{\pi}{4}\)
B. \(x=\frac{\pi}{6}\)
C. \(x=0\,\, và \,\,x=\frac{\pi}{2}\)
D. \(x=\frac{\pi}{3}\)
-
Câu 50:
Hàm số \(y=\sqrt{1+x^{2}}+\sqrt{1-x^{2}}\) đạt giá trị nhỏ nhất lần lượt tại hai điểm có hoành độ:
A. 0
B. \(±1\)
C. \(\pm \sqrt{2}\)
D. 2
