Trắc nghiệm Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán Lớp 12

Câu 1:

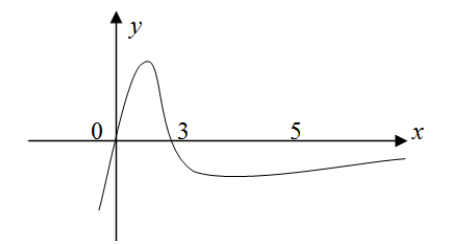
Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ bên dưới. Biết rằng m là tham số thực, giá trị nhỏ nhất của hàm số \(g\left( x \right) = f\left( x \right) + {x^2} – 2mx + {m^2} + 1\) tương ứng bằng:

Câu 2:

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) sao cho \(\mathop {{\rm{max}}}\limits_{x \in \left[ {0;10} \right]} \,f\left( x \right) = f\left( 2 \right) = 4.\) Xét hàm số \(g\left( x \right) = f\left( {{x^3} + x} \right) – {x^2} + 2x + m.\) Giá trị của tham số m để \(\mathop {{\rm{max}}}\limits_{x \in \left[ {0;2} \right]} \,g\left( x \right) = 8\) là

Câu 3:

Cho hàm số y = f(x) có đồ thị như hình bên. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình f(\sin x) = m có đúng hai nghiệm thuộc đoạn \([0;\pi ]?\)

Câu 4:

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị trên đoạn \(\left[ {0;4} \right]\) như hình vẽ bên dưới

Đặt \(M = \max f\left( {\sqrt {4 – {x^2}} } \right),m = \min f\left( {\sqrt {4 – {x^2}} } \right)\). Tổng M + m bằng

Câu 5:

Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f’\left( x \right)\) có bảng biến thiên như sau:

Bất phương trình \(f\left( x \right) < {x^3} + m\) đúng với mọi \(x \in \left( { – 1\,;\,1} \right)\) khi và chỉ khi

Câu 6:

Cho hàm số y = f(x) có bảng biến thiên như sau:

Tất cả các giá trị của m để bất phương trình \(f\left( {\sqrt {x – 1} + 1} \right) \le m\) có nghiệm là

Câu 7:

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên dưới.

Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số \(g\left( x \right) = f\left( {2\sin \frac{x}{2}\cos \frac{x}{2} + 3} \right)\) trên \(\mathbb{R}.\) Giá trị của M + m bằng

Câu 8:

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên trên đoạn \(\left[ { – 1;4} \right]\) như sau:

Giá trị lớn nhất của hàm số \(y = \left| {f\left( x \right)} \right|\) trên đoạn đoạn \(\left[ { – 1;4} \right]\) bằng

Câu 9:

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên trên đoạn \(\left[ { – 1;4} \right]\) như sau:

Giá trị lớn nhất của hàm số \(y = \left| {f\left( x \right)} \right|\) trên đoạn đoạn \(\left[ { – 1;4} \right]\) bằng

Câu 10:

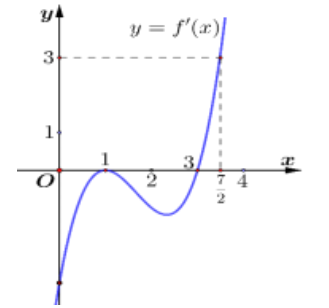
Cho hàm số y = f(x) có đạo hàm y = f'(x) liên tục trên \(\mathbb{R}\) và có đồ thị của hàm số y = f'(x) trên đoạn \(\left[ { – 2;6} \right]\) như hình vẽ bên.Cho hàm số y = f(x) có đạo hàm y = f'(x) liên tục trên \(\mathbb{R}\) và có đồ thị của hàm số y = f'(x) trên đoạn \(\left[ { – 2;6} \right]\) như hình vẽ bên.

Tìm khẳng định đúng trong các khẳng định sau:

Câu 11:

Cho hàm số \(y = f\left( x \right)\), hàm số \(f’\left( x \right)\) có đồ thị như hình vẽ

Giá trị nhỏ nhất của hàm số \(g\left( x \right) = \frac{1}{2}f\left( {2x – 1} \right) + \frac{{11}}{{19}}{\left( {2x – 1} \right)^2} – 4x\) trên khoảng \(\left[ {0;\frac{5}{2}} \right]\) bằng

Câu 12:

Cho hàm số \(y = f\left( x \right)\) có đạo hàm cấp 2 trên \(\mathbb{R}\), hàm số \(y = f’\left( x \right)\) có đồ thị như hình vẽ bên.

Giá trị lớn nhất của hàm số \(y = f\left( {\frac{{\sin x + \sqrt 3 \cos x}}{2}} \right)\) trên đoạn \(\left[ { – \frac{{5\pi }}{6}\,;\,\frac{\pi }{6}} \right]\) bằng

Câu 13:

Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số \(g\left( x \right) = f\left( {4x – {x^2}} \right) + \frac{1}{3}{x^3} – 3{x^2} + 8x + \frac{1}{3}\) trên đoạn \(\left[ {1\,;\,3} \right]\).

Câu 14:

Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right)\). Hàm số \(y = f’\left( x \right)\) liên tục trên tập số thực và có đồ thị như hình vẽ.

Biết \(f\left( { – 1} \right) = \frac{{13}}{4},\,f\left( 2 \right) = 6\). Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(g\left( x \right) = {f^3}\left( x \right) – 3f\left( x \right)\) trên \(\left[ { – 1;2} \right]\) bằng

Câu 15:

Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị hàm số \(y = f’\left( x \right)\) như hình vẽ bên. Gọi \(g\left( x \right) = f\left( x \right) – \frac{1}{3}{x^3} + \frac{1}{2}{x^2} + x – 2019\). Biết \(g\left( { – 1} \right) + g\left( 1 \right) > g\left( 0 \right) + g\left( 2 \right)\).

Với \(x \in \left[ { – 1;\,\,2} \right]\) thì \(g\left( x \right)\) đạt giá trị nhỏ nhất bằng

Câu 16:

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị hàm số đạo hàm \(y = f’\left( x \right)\) như hình vẽ.

Xét hàm số \(g\left( x \right) = f\left( x \right) – \frac{1}{3}{x^3} – \frac{3}{4}{x^2} + \frac{3}{2}x + 2021\). Mệnh đề nào dưới đây đúng?

Câu 17:

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\). Đồ thị của hàm số \(y = f’\left( x \right)\) như hình vẽ dưới đây.

Xét hàm số \(g\left( x \right) = 2f\left( x \right) – {\left( {x + 1} \right)^2}\). Mệnh đề nào sau đây là đúng?

Câu 18:

Cho hàm số f(x). Biết hàm số y = f'(x) có đồ thị như hình bên. Trên đoạn \({\rm{[}} – 4;3]\), hàm số \(g(x) = 2f(x) + {(1 – x)^2}\) đạt giá trị nhỏ nhất tại điểm.

Câu 19:

Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số \(y = f’\left( x \right)\) như hình vẽ

Đặt \(g\left( x \right) = \frac{1}{3}{x^3} – x – f\left( x \right) + 2020\). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ { – \sqrt 3 ;\,\sqrt 3 } \right]\). Hãy tính M + m.

Câu 20:

Cho hàm số \(y = f\left( x \right)\) có đồ thị \(f’\left( x \right)\) như hình vẽ

Giá trị nhỏ nhất của hàm số \(g\left( x \right) = f\left( x \right) + \frac{1}{3}{x^3} – x\) trên đoạn \(\left[ { – 1;2} \right]\) bằng

Câu 21:

Cho hàm số \(f\left( x \right)\), đồ thị của hàm số \(y = f’\left( x \right)\) là đường cong trong hình bên. Giá trị lớn nhất của hàm số \(g\left( x \right) = f\left( {2x} \right) – 4x\) trên đoạn \(\left[ { – \frac{3}{2};2} \right]\) bằng

Câu 22:

Nếu hàm số \(y=x+m+\sqrt{1-x^{2}}\) có giá trị lớn nhất bằng \(2 \sqrt{2}\) thì giá trị của m là 

Câu 23:

Cho hàm số \(y=2 x^{3}-3 x^{2}-m\) . Trên \([-1 ; 1]\) hàm số có giá trị nhỏ nhất là -1 . Tính m

Câu 24:

Cho \(x, y \in \mathbb{R} \text { thỏa } \text { mãn } x+y \neq-1\) và \(x^{2}+y^{2}+x y=x+y+1\). Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P=\frac{x y}{x+y+1}\). Tính M+m.

Câu 25:

Cho hai số thực x y , thay đổi thỏa mãn điều kiện \(x^{2}+y^{2}=2\) . Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức \(P=2\left(x^{3}+y^{3}\right)-3 x y\) . Giá trị của M + n bằng: 

Câu 26:

Cho \(x^{2}-x y+y^{2}=2 \text { . }\)Giá trị nhỏ nhất của \(P=x^{2}+x y+y^{2} b\) bằng 

Câu 27:

Cho hàm số y=f(x) có đạo hàm \(f^{\prime}(x)\). Hàm số \(y=f^{\prime}(x)\) liên tục trên tập số thực và có bảng biến thiên như sau: 

Biết rằng \(f(-1)=\frac{10}{3}, f(2)=6\). Giá trị nhỏ nhất của hàm số \(g(x)=f^{3}(x)-3 f(x)\) trên đoạn \([-1 ; 2]\) bằng?

Câu 28:

Cho hàm số y=f(x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số\(g(x)=f\left(4 x-x^{2}\right)+\frac{1}{3} x^{3}-3 x^{2}+8 x+\frac{1}{3}\)  trên đoạn [1;3]?

Câu 29:

Cho hàm số có f(x) có đạo hàm là hàm \(f^{\prime}(x)\). Đồ thị hàm số \(f^{\prime}(x)\) như hình vẽ bên. Biết rằng \(f(0)+f(1)-2 f(2)=f(4)-f(3)\) . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4]?

Câu 30:

Cho hàm số f(x) có đạo hàm là \(f^{\prime}(x)\) . Đồ thị của hàm số \(y=f^{\prime}(x)\) được cho như hình vẽ bên. Biết rằng \(f(0)+f(1)-2 f(3)=f(5)-f(4) .\) Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;5]?
 

Câu 31:

Cho hàm số y =f(x) liên tục trên \(\left[0 ; \frac{7}{2}\right]\) có đồ thị hàm số y=f'(x) như hình vẽ sau: 

Hàm số y=f(x) đạt giá trị nhỏ nhất trên \(\left[0 ; \frac{7}{2}\right]\) tại điểm x₀ nào dưới đây?
 

Câu 32:

Cho hàm số y=f(x) xác định và liên tục trên \(\mathbb{R}\), đồ thị của hàm số \(y=f^{\prime}(x)\) như hình vẽ sau:

Giá trị lớn nhất của hàm số \(y=f(x) \text { trên đoạn }[-1 ; 2]\) là?

Câu 33:

Cho hàm số y=f(x) có đạo hàm \(f^{\prime}(x)=-x(x-2)^{2}(x-3), \forall x \in \mathbb{R}\) . Giá trị lớn nhất của hàm số đã cho trên đoạn [0 ; 4] bằng:

Câu 34:

Tổng giá trị lớn nhất M và giá trị nhỏ nhất của hàm số \(f(x)=(x-6) \sqrt{x^{2}+4}\) trên đoạn [0;3] có dạng \(a-b \sqrt{c}\) với a là số nguyên và b , c là các số nguyên dương. Tính \(S=a+b+c\).

Câu 35:

Giá trị nhỏ nhất của hàm số \(f(x)=(x+1)(x+2)(x+3)(x+4)+2019\) là?

Câu 36:

Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f(x)=x-\sqrt{x}\) trên đoạn [ 0; 3] . Giá trị của biểu thức \(M+2 m\) gần với số nào nhất trong các số dưới đây ?

Câu 37:

Tính giá trị nhỏ nhất của hàm số \(y=3 x+\frac{4}{x^{2}}\) trên khoảng \((0 ;+\infty) \text { . }\)

Câu 38:

Tìm x để hàm số \(y=x+\sqrt{4-x^{2}}\) đạt giá trị lớn nhất. 

Câu 39:

Tìm giá trị nhỏ nhất m của hàm số \(y=x^{4}-x^{2}+13\) trên đoạn [-2;3].

Câu 40:

Gọi M là giá trị lớn nhất của hàm số \(\begin{equation} f(x)=4 \sqrt{x^{2}-4 x+6}+4 x-x^{2}+1 \end{equation}\) . Tính tích các nghiệm của phương trình f(x)=M?

Câu 41:

Gọi M và m lầ lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(\begin{equation} f(x)=2 x-4 \sqrt{6-x} \end{equation}\) trên \(\begin{equation} [-3 ; 6] \end{equation}\). Tổng M+m có giá trị là: 

Câu 42:

Tìm giá trị nhỏ nhất của hàm số \(y=x^{2}+\frac{2}{x}\) trên đoạn \(\left[\frac{1}{2} ; 2\right]\)

Câu 43:

Giá trị nhỏ nhất của hàm số \(f(x)=x^{3}-3 x\) trên đoạn \([-3 ; 3]\) bằng?

Câu 44:

Tìm giá trị lớn nhất M của hàm số \(y=x^{4}-2 x^{2}+3\) trên đoạn \([0 ; \sqrt{3}] .\)

Câu 45:

Giá trị nhỏ nhất của hàm số \(y=3 \cos 2 x-4 \sin x\) là?

Câu 46:

Giá trị lớn nhất của hàm số \(y=2 \sin ^{2} x-\cos x\) là phân số tối giản có dạng với a, b là các số nguyên dương. Tìm a-b?

Câu 47:

Cho hàm số là \(f(x)=\cos 2 x-\cos x+1\). Giá trị nhỏ nhất của hàm số trên \(\mathbb{R}\) là?

Câu 48:

Cho hàm số \(f(x)=\sin ^{3} x-3 \sin x+2 .\) Gọi và lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho.
Khi đó là \(M+2 m\) là?

Câu 49:

Giá trị nhỏ nhất của hàm số \(y=\frac{2 \sin x+3}{\sin x+1} \text { trên đoạn }\left[0 ; \frac{\pi}{2}\right]\)

Câu 50:

Giá trị lớn nhất của hàm số \(y=\sqrt{-x^{2}+5 x}\) bằng