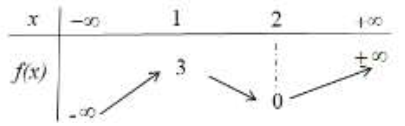
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f’\left( x \right)\) có bảng biến thiên như sau:

Bất phương trình \(f\left( x \right) < {x^3} + m\) đúng với mọi \(x \in \left( { – 1\,;\,1} \right)\) khi và chỉ khi

Trong số các hình chữ nhật có cùng chu vi 16 cm, hình chữ nhật có diện tích lớn nhất bằng:

Hàm số \(y=x^{8}+\left(x^{4}-1\right)^{2}\) đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [1;2] lần lượt tại hai điểm có hoành độ \(x_{1} ; x_{2}\). Khi đó tích \(x_{1} . x_{2}\) có giá trị bằng
 

Gọi m và M lần lượt là các giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(f\left( x \right) = {{\rm{e}}^{2 – 3x}}\) trên đoạn \(\left[ {0;2} \right]\). Mối liên hệ giữa M và m là

Tìm tất cả các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số \(y = \frac{{x + 2{m^2} – m}}{{x – 3}}\) trên đoạn \(\left[ {0;1} \right]\) bằng – 2.

Cho hàm số y = f(x) có đạo hàm y = f'(x) liên tục trên \(\mathbb{R}\) và có đồ thị của hàm số y = f'(x) trên đoạn \(\left[ { – 2;6} \right]\) như hình vẽ bên.Cho hàm số y = f(x) có đạo hàm y = f'(x) liên tục trên \(\mathbb{R}\) và có đồ thị của hàm số y = f'(x) trên đoạn \(\left[ { – 2;6} \right]\) như hình vẽ bên.

Tìm khẳng định đúng trong các khẳng định sau:

Xét hàm số \(y = \frac{{{x^2}}}{{x - 1}}\)

Trong các khẳng định sau, khẳng định nào là đúng?

Hàm số \(y=\cos ^{2} x-2 \cos x-1\) có giá trị nhỏ nhất và giá trị lớn nhất trên đoạn \([0 ; \pi]\)lần lượt bằng \(y_{1} ; y_{2}\) . Khi đó tích \(y_{1} . y_{2}\) có giá trị bằng:

Một hành lang giữa hai tòa tháp có hình dạng một hình lăng trụ đứng. Hai mặt bên ABB’A’ và ACC’A’ là hai tấm kính hình chữ nhật dài 20m, rộng 5m. Với độ dài xấp xỉ nào của BC thì thể tích hành lang này lớn nhất

Giá trị lớn nhất M, giá trị nhỏ nhất m của hàm số:\(y=2 \sin ^{2} x+2 \sin x-1\) là:

Hàm số \(y=\sqrt{1+2 \sin x \cdot \cos x}\) đạt giá trị nhỏ nhất trên đoạn \(\left[0 ; \frac{\pi}{2}\right]\) tại điểm có hoành độ là:

Giá trị nhỏ nhất của hàm số \(y=e^{x}\left(x^{2}-3\right)\) trên đoạn [-2;2]

Cho hàm số \(\begin{equation} y=f(x) \end{equation}\) có bảng biến thiên như sau:

Khẳng định nào sau đây đúng?

Giá trị nhỏ nhất của hàm số \(y=e^{x}\left(x^{2}-3\right)\) trên đoạn [-2;2] là
 

Cho hàm số y=f(x) xác định, liên tục trên và có bảng biến thiên như sau: 

Giá trị lớn nhất của hàm số y=f(x) trên đoạn [ 0; 2] bằng:

Giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y=\frac{x-1}{2x+1}\)trên đoạn [1;3] là:

Hàm số \(y=\sqrt{1+x^{2}}+\sqrt{1-x^{2}}\) đạt giá trị nhỏ nhất lần lượt tại hai điểm có hoành độ:

Giá trị lớn nhất của hàm số \(y=2 \sin x-\frac{4}{3} \sin ^{3} x \text { trên }[0 ; \pi]\) là:

Tìm tập giá trị T của hàm số \(y = x + \sqrt {4 – {x^2}} .\).

Kết luận nào là đúng về giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{x-x^{2}} ?\)

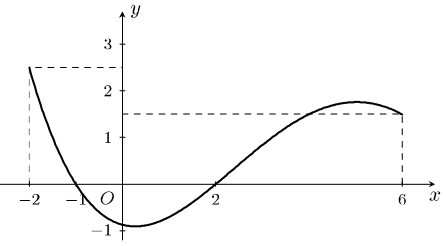
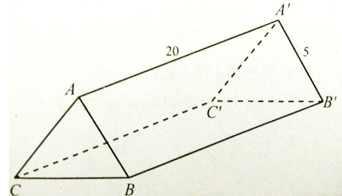
Giá trị nhỏ nhất của hàm số \(y=3+\sqrt{x^{2}-2 x+5}\) bằng