ADMICRO
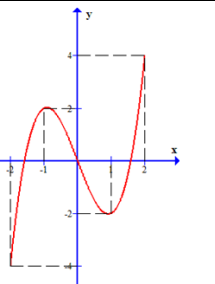
Tìm điểm cực đại của đồ thị hàm số y = x³ - 3x + 2.
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Môn: Toán Lớp 12
Bài: Cực trị của hàm số
ZUNIA12
Lời giải:
Báo sai
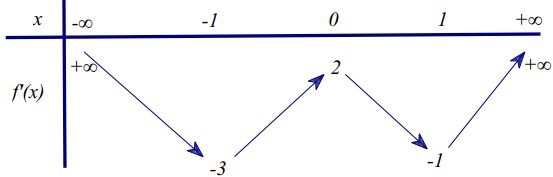
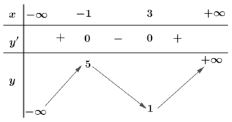
Bảng biến thiên
.png)
Hàm số đạt cực đại tại
Vậy điểm cực đại của đồ thị hàm số là (-1;4)
ZUNIA9
AANETWORK



.jpg.png)











