Đề Thi Tham Khảo Đánh Giá Năng Lực Năm 2024 – ĐHQG Hà Nội – Đề Số 01 - Phần 1: Toán Học Và Xử Lí Số Liệu/Tư Duy Định Lượng
Câu 1
Trong hệ trục tọa độ Oxy , cho đường thẳng \(d:\left\{\begin{array}{l}x=-4 t+1 \\ y=-2+3 t\end{array}\right.\). Một vectơ chỉ phương của \(d\) là:
A.\((1; 3)\).
B.\((-4;2)\).
C.\((4;-3)\).
D.\((-1; 3)\).
Câu 3
Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \(x^{2}-(m+2) x+8 m+1 \leq 0\) vô nghiệm.
A.\(m \in[0; 28]\).
B.\(m \in(0; 28)\).
C.\(m \in(-\infty; 0) \cup(28;+\infty)\).
D.\(m \in(-\infty; 0] \cup[28;+\infty)\).
Câu 4
Số cách xếp 5 học sinh ngồi vào một dãy gồm 5 chiếc ghế sao mỗi ghế có đúng một học sinh ngồi là
A.600.
B.120.
C.3125.
D.720.
Câu 8
Biết bất phương trình \(\log _{2}\left(3^{x}-3\right) \log _{8}\left(3^{x} 2^{-2}-\frac{3}{4}\right) \leq 1\) có tập nghiệm là đoạn [ \(\mathrm{a}; \mathrm{b}\) ]. Giá trị biểu thức \(a+b\) bằng
A.\(1+\log _{3} 77\).
B.\(\log _{3} \frac{77}{2}\).
C.\(-2+\log _{2} \frac{77}{2}\).
D.\(-1+\log _{2} 77\).
Câu 10
Cho hình chóp \(\mathrm{S}. \mathrm{ABC}\) có đáy ABC là tam giác vuông tại \(\mathrm{B}, \mathrm{SA}\) vuông góc với mặt đáy và \(S A=A B=\sqrt{3}\). Gọi \(G\) là trọng tâm của tam giác SAB. Khoảng cách từ \(G\) đến mặt phẳng \((S B C)\) bằng:
A.\(\frac{\sqrt{6}}{3}\).
B.\(\frac{\sqrt{6}}{6}\).
C.\(\sqrt{3}\).
D.\(\frac{\sqrt{6}}{2}\).
Câu 12
Tìm các đường tiệm cận của đồ thị hàm số \(y=\frac{\sqrt{x^{2}-4}}{x-1}\).
A.\(x=1; y=1\).
B.\(x=1; y=-1; y=1\).
C.\(y=-1; y=1\).
D.\(x=1; x=2; y=1\).
Câu 14
Tập giá trị của hàm số \(y=\frac{\sin 3 x-2 \cos 3 x+10}{6 \cos x \cos 2 x-4 \cos ^{3} x+3}\) có bao nhiêu số nguyên?
A.10.
B.11.
C.12.
D.13.
Câu 15
Biểu đồ dưới đây thể hiện tỉ lệ lạm phát cơ bản bình quân năm trong giai đoạn 2018 - 2022:
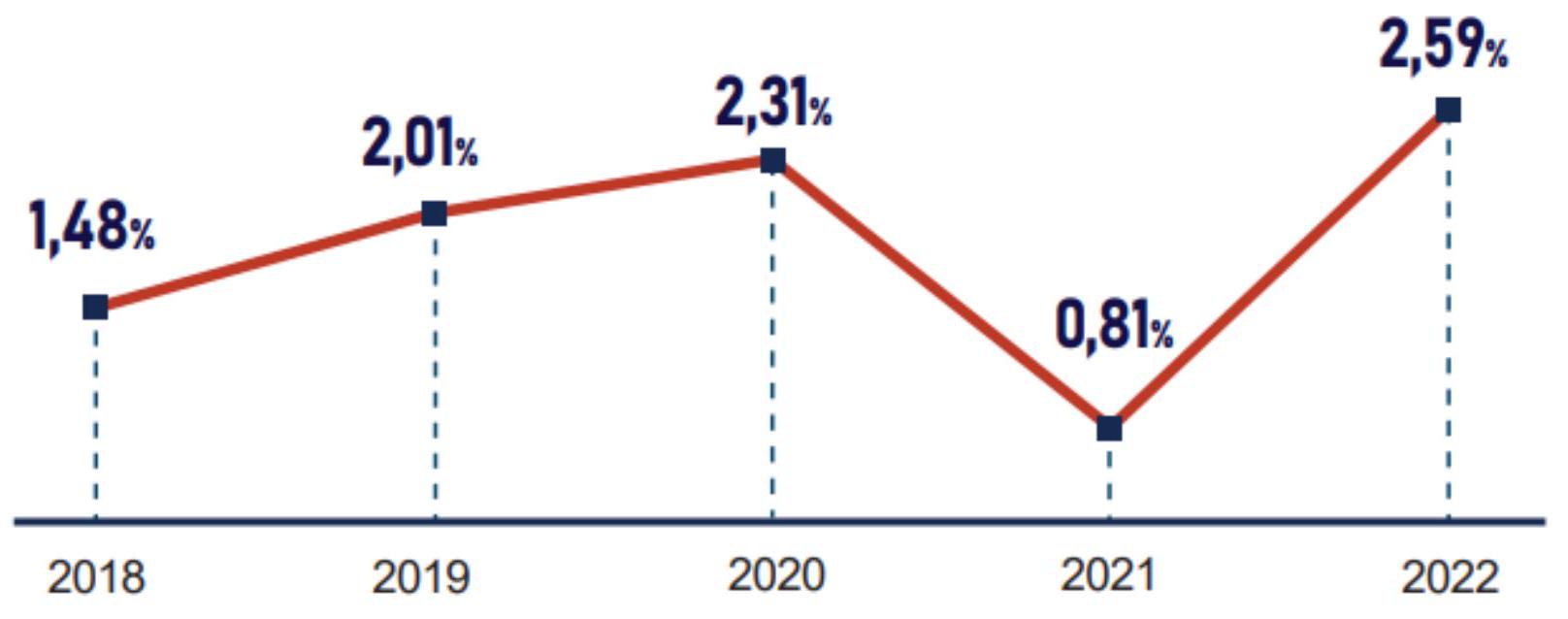(Nguồn: Niêm giám thống kê 2022)Trong giai đoạn từ 2018 - 2021, năm có tỉ lệ lạm phát cơ bản bình quân năm cao nhất là?
A.Năm 2022.
B.Năm 2019.
C.Năm 2021.
D.Năm 2020.
Câu 16
Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức \(h(t)=29+3 \sin \frac{\pi}{12}(t-9)\) với \(h\) tính bằng \({ }^{\circ} C\) và \(t\) là thời gian trong ngày tính bằng giờ. Thời gian nhiệt độ cao nhất trong ngày là:
A.13 giờ.
B.15 giờ.
C.12 giờ.
D.14 giờ.
Câu 17
Hai cậu bé cùng bắn bi vào lỗ. Xác suất người thứ nhất bắn trúng vào lỗ là \(85 \%\), xác suất người thứ hai bắn trúng vào lỗ là \(70 \%\). Hỏi xác suất để cả hai người cùng bắn trúng vào lỗ:
A.\(59,5 \%\).
B.\(15 \%\).
C.\(30 \%\).
D.\(4,5 \%\).
Câu 19
Cho lăng trụ đứng \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có đáy \(ABC\) là tam giác đều cạnh \(a\). Gọi \(D\) là trung điểm cạnh \(BC\). Biết \(A A^{\prime}=2 a\), khoảng cách giữa hai đường thẳng \(A^{\prime} B\) và \(C^{\prime} D\) là:
A.\(a \sqrt{17}\).
B.\(\frac{a}{\sqrt{17}}\).
C.\(2 a \sqrt{17}\).
D.\(\frac{2 a}{\sqrt{17}}\).
Câu 21
Cho phương trình \((m-1) x^{4}+2(m-3) x^{2}+m+3=0\) ( \(m\) là tham số). Tìm \(m\) để phương trình vô nghiệm.
A.\(m \in(-\infty;-3) \cup\left(\frac{3}{2};+\infty\right)\).
B.\(m \leq-3\).
C.\(m>\frac{3}{2}\).
D.\(m<-3\).
Câu 22
Cho hàm số \(f(x)=k \sqrt[3]{x}+\sqrt{x}\). Với giá trị nào của \(k\) thì \(f^{\prime}(1)=\frac{3}{2}\) ?
A.\(k=1\).
B.\(k=\frac{9}{2}\).
C.\(k=-3\).
D.\(k=3\).
Câu 24
Cho hàm số \(f(x)\) có đạo hàm trên \(\mathbb{R}\) và \(f^{\prime}(x)<0, \forall x \in(0;+\infty)\) biết \(f(0)=3\). Khẳng định nào sau đây có thể xảy ra.
A.\(f(2024)=3,5\).
B.\(f(2023)+f(2024)=6\).
C.\(f(2023)<f(2024)\).
D.\(f(-2024)=3\).
Câu 25
Phương trình đường tròn có tâm thuộc đường thẳng \(\Delta: x-2 y=0\), tiếp xúc với đường thẳng \(\Delta^{\prime}: 2 x-y+2=0\) đồng thời đường tròn đi qua điểm \(M(1; 3)\) là:
A.\((x+2)^{2}+(y+1)^{2}=5\) và \(\left(x+\frac{23}{4}\right)^{2}+\left(y+\frac{23}{8}\right)^{2}=\frac{1445}{64}\).
B.\((x-2)^{2}+(y-1)^{2}=5\) và \(\left(x-\frac{23}{4}\right)^{2}+\left(y-\frac{23}{8}\right)^{2}=\frac{1445}{64}\).
C.\((x+1)^{2}+(y-1)^{2}=5\) và \(\left(x-\frac{23}{4}\right)^{2}+\left(y-\frac{23}{8}\right)^{2}=\frac{1445}{64}\).
D.\((x-2)^{2}+(y-1)^{2}=5\) và \(\left(x-\frac{23}{4}\right)^{2}+\left(y-\frac{23}{8}\right)^{2}=\frac{1885}{16}\).
Câu 26
Khoảng cách giữa hai điểm cực trị của đồ thị hàm số \(y=(x-2)^{2}(x+1)\) là
A.\(2 \sqrt{5}\).
B.\(5 \sqrt{2}\).
C.4.
D.2.
Câu 28
Với số nguyên dương \(n\), gọi \(a_{3 n-3}\) là hệ số của \(x^{3 n-3}\) trong khai triển thành đa thức của \(\left(x^{2}+1\right)^{n}(x+2)^{n}\). Tìm \(n\) để \(a_{3 n-3}=26 n\).
A.\(n=6\).
B.\(n=7\).
C.\(n=5\).
D.\(n=4\).
Câu 29
Chọn ngẫu nhiên lần lượt các số \(a, b\) phân biệt thuộc tập hợp \(\left\{3^{k} \mid k \in \mathbb {N}, 1 \leq k \leq 10\right\}\). Tính xác suất để \(\log _{a} b\) là một số nguyên dương.
A.\(\frac{17}{90}\).
B.\(\frac{17}{45}\).
C.\(\frac{3}{10}\).
D.\(\frac{22}{45}\).
Câu 30
Cho các số thực \(\mathrm{a}, \mathrm{b}, \mathrm{c}\) thỏa mãn \(c^{2}+a=18\) và \(\lim _{x \rightarrow+\infty}\left(\sqrt{a x^{2}+b x}-c x\right)=-2\). Tính giá trị biểu thức \(P=a+b+5 c\).
A.\(P=18\).
B.\(P=12\).
C.\(P=9\).
D.\(P=5\).
Câu 31
Gọi \(S\) là tập hợp các số tự nhiên có 6 chữ số. Chọn ngẫu nhiên một số từ \(S\), xác suất để các chữ số của số đó đôi một khác nhau và phải có mặt chữ số 0 và 1 bằng
A.\(\frac{7}{150}\).
B.\(\frac{7}{375}\).
C.\(\frac{7}{125}\).
D.\(\frac{189}{1250}\).
Câu 33
Cho hình chóp \(\mathrm{S}. \mathrm{ABCD}\) có đáy \(ABCD\) là hình bình hành. Mặt phẳng \((\alpha)\) qua \(BD\) và song song với \(SA\), mặt phẳng \((\alpha)\) cắt \(SC\) tại \(K\). Tính tỉ số \(\frac{S K}{K C}\).
A.\(\frac{S K}{K C}=2\).
B.\(\frac{S K}{K C}=3\).
C.\(\frac{S K}{K C}=1\).
D.\(\frac{S K}{K C}=\frac{1}{2}\).
Câu 35
Cho tứ diện \(ABCD\) có \(BCD\) là tam giác vuông tại đỉnh \(B\), cạnh \(C D=a, B D=\frac{a \sqrt{6}}{3}\), \(A B=A C=A D=\frac{a \sqrt{3}}{2}\). Tính cosin của góc nhị diện \([\mathrm{A}, \mathrm{BC}, \mathrm{D}]\).
A.\(\frac{\sqrt{2}}{2}\).
B.\(\frac{1}{2}\).
C.\(\frac{\sqrt{3}}{2}\).
D.\(-\frac{1}{2}\).
Câu 37
Nghiệm của phương trình \(2^{2 x-1}=8\) là:
A.\(x=2\).
B.\(x=1\).
C.\(x=4\).
D.\(x=\frac{5}{2}\).
Câu 39
Một vật chuyển động theo quy luật \(s=-\frac{1}{2} t^{3}+9 t^{2}\) với \(t\) (giây) là khoảng thời gian tính từ lúc bắt đầu chuyển động và \(s\) (mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
A.\(216~(\mathrm{m} / \mathrm{s})\).
B.\(30~(\mathrm{m} / \mathrm{s})\).
C.\(400~(\mathrm{m} / \mathrm{s})\).
D.\(54~(\mathrm{m} / \mathrm{s})\)
Câu 40
Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng \(d:\left\{\begin{array}{l}x=2+t y=1-3 t\end{array}\right.\) và hai điểm \(A(1; 2), B(-2; m)\). Tìm tất cả các giá trị của tham số \(m\) để \(A\) và \(B\) nằm cùng phía đối với \(d\).
A.\(m>13\).
B.\(m \geq 13\).
C.\(m<13\).
D.\(m=13\).
Câu 43
Cho cấp số cộng \(\left(u_{n}\right)\) có \(u_{1}=4\). Giá trị nhỏ nhất của \(u_{1} u_{2}+u_{2} u_{3}+u_{3} u_{1}\) bẳng:
A.-8.
B.-24.
C.-20.
D.-6.
Câu 44
Cho cấp số nhân \(\left(u_{n}\right)\) có \(u_{2}=-6, u_{5}=48\). Tính \(S_{5}\).
A.33.
B.-31.
C.93.
D.11.
Câu 45
Năng lượng giải tỏa \(E\) của một trận động đất tại tâm địa chấn \(M\) độ Richter được xác định bởi công thức \(\log E=11,4+1,5 M\). Vào năm 1995, thành phố \(X\) xảy ra một trận động đất 8 độ Richter và năng lượng giải tỏa tại tâm địa chấn của nó gấp 14 lần trận động đất ra tại thành phố \(Y\) vào năm 1997. Hỏi khi đó độ lớn của trận động đất tại thành phố \(Y\) là bao nhiêu? (kết quả làm tròn đến hàng phần chục)
A.7,2 độ Richter.
B.7,8 độ Richter.
C.8,3 độ Richter.
D.6,8 độ Richter.
Câu 47
Hàm số \(y=3 \cos \left(\frac{\pi}{4}-m x\right)\) tuần hoàn có chu kì \(T=3 \pi\) khi
A.\(m= \pm \frac{3}{2}\)
B.\(m= \pm 1\)
C.\(m= \pm \frac{2}{3}\)
D.\(m= \pm 2\)
Câu 49
Giả sử \(x_{1}, x_{2}\) là nghiệm của phương trình \(x^{2}-(m+2) x+m^{2}+1=0\). Khi đó giá trị lớn nhất của biểu thức \(P=4\left(x_{1}+x_{2}\right)-x_{1} x_{2}\) bằng:
A.\(\frac{95}{9}\).
B.11.
C.7.
D.\(-\frac{1}{9}\).
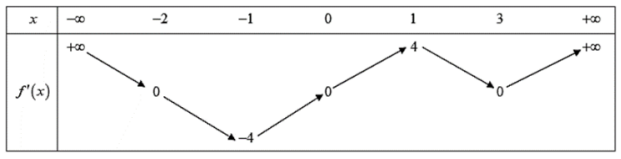
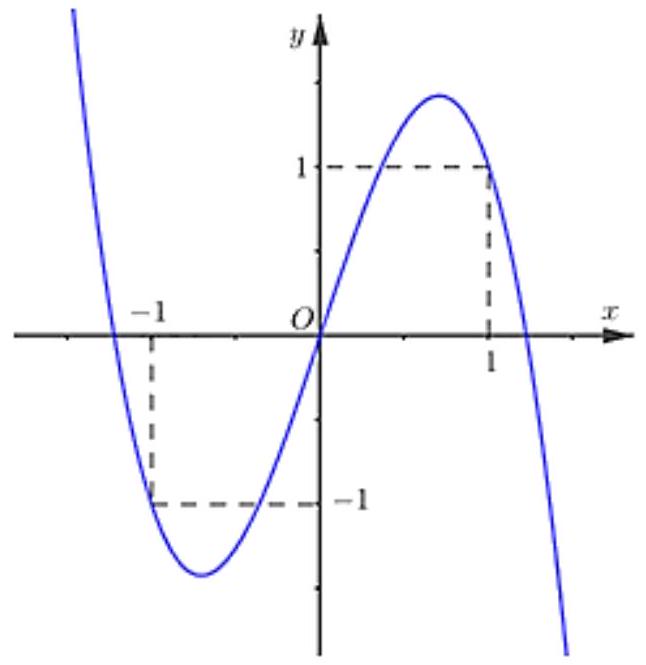Hàm số \(y=\left|f(x)-\frac{x^{2}}{2}\right|\) có bao nhiêu điểm cực trị?
Top 10/0 lượt thi
| Tên | Điểm | Thời gian |
|---|
