Đề thi HK1 môn Toán 10 năm 2020
Trường THPT Thủ Khoa Huân
-
Câu 1:
Trong các mệnh đề sau đây, mệnh đề nào có mệnh đề đảo là đúng?
A. Nếu a và b cùng chia hết cho c thì a + b chia hết cho c.
B. Nếu hai tam giác bằng nhau thì diện tích bằng nhau.
C. Nếu a chia hết cho 3 thì a chia hết cho 9.
D. Nếu một số tận cùng bằng 0 thì số đó chia hết cho 5.
-
Câu 2:
Trong các mệnh đề sau, mệnh đề nào không phải là định lí?
A. \(\exists x \in N,{\rm{ }}{x^2}\) chia hết cho 3 ⇒ x chia hết cho 3.
B. \(\exists x \in N,{\rm{ }}{x^2}\) chia hết cho 6 ⇒ x chia hết cho 3.
C. \(\forall x \in N ,{\rm{ }}{x^2}\) chia hết cho 9 ⇒ x chia hết cho 9.
D. \(\exists x \in N,{\rm{ }}x\) chia hết cho 4 và 6 ⇒ x chia hết cho 12
-
Câu 3:
Trong các tập hợp sau, tập nào là tập rỗng?
A. \({T_1} = \left\{ {x \in N|{x^2} + 3x - 4 = 0} \right\}\)
B. \({T_1} = \left\{ {x \in N |{x^2} - 3 = 0} \right\}\)
C. \({T_1} = \left\{ {x \in N|{x^2} = 2} \right\}\)
D. \({T_1} = \left\{ {x \in Q|\left( {{x^2} + 1} \right)\left( {2x - 5} \right) = 0} \right\}\)
-
Câu 4:
Cho các tập hợp \(A = \left\{ {x \in R|\,x < 3} \right\}\), \(B = \left\{ {x \in R|1 < x \le 5} \right\}\), \(C = \left\{ {x \in R| - 2 \le x \le 4} \right\}\). Tính \(\left( {B \cup C} \right)\backslash \left( {A \cap C} \right).\)
A. [-2; 3)
B. [3; 5]
C. \(\left( { - \infty ;\,1} \right]\)
D. [-2; 5]
-
Câu 5:
Cho \(A = \left( { - \infty ;2} \right]\), \(B = \left[ {2; + \infty } \right)\), \(C = \left( {0;3} \right)\). Chọn phát biểu sai.
A. \(A \cap C = \left( {0;2} \right]\)
B. \(B \cup C = \left( {0; + \infty } \right)\)
C. \(A \cup B = R\backslash \left\{ 2 \right\}\)
D. \(B \cap C = \left[ {2;3} \right)\)
-
Câu 6:
Cho số thực a < 0. Tìm điều kiện cần và đủ để \(\left( { - \infty ;9a} \right) \cap \left( {\frac{4}{a}; + \infty } \right) \ne \emptyset \).
A. \( - \frac{2}{3} < a < 0\)
B. \( - \frac{3}{4} < a < 0\)
C. \( - \frac{2}{3} \le a < 0\)
D. \(- \frac{3}{4} \le a < 0\)
-
Câu 7:
Tập hợp nào dưới đây là giao của hai tập hợp \(A = \left\{ {x \in : - 1 \le x < 3} \right\}\), \(B = \left\{ {x \in R:\left| x \right| < 2} \right\}\)?
A. (-1; 2)
B. [0; 2)
C. (-2; 3)
D. [-1; 2)
-
Câu 8:
Cho \(A = \left[ {1; + \infty } \right)\), \(B = \left\{ {x \in R|{x^2} + 1 = 0} \right\}\), \(C = \left( {0;4} \right)\). Tập \(\left( {A \cup B} \right) \cap C\) có bao nhiêu phần tử là số nguyên.
A. 3
B. 1
C. 0
D. 2
-
Câu 9:
Phương trình \(\left| {3x - 1} \right| = 2x - 5\) có bao nhiêu nghiệm?
A. Vô số
B. 1
C. 0
D. 2
-
Câu 10:
Cho tam giác ABC có G là trọng tâm. Mệnh đề nào sau đây sai?
A. \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \) với mọi điểm M
B. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
C. \(\overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GA} \)
D. \(3\overrightarrow {AG} = \overrightarrow {AB} + \overrightarrow {AC} \)
-
Câu 11:
Trong mặt phẳng Oxy, cho \(A\left( {2; - 3} \right)\), \(B\left( {3;4} \right)\). Tìm tọa độ điểm M nằm trên trục hoành sao cho A, B, M thẳng hàng.
A. M(1;0)
B. M(4;0)
C. \(M\left( { - \frac{5}{3}; - \frac{1}{3}} \right)\)
D. \(M\left( {\frac{{17}}{7};0} \right)\)
-
Câu 12:
Theo thống kê, dân số Việt Nam năm 2016 được ghi lại như sau \(\overline S = 94\,\,444\,\,200 \pm 3000\) (người). Số quy tròn của số gần đúng \(94\,\,444\,\,200\) bằng bao nhiêu?
A. 94 440 000
B. 94 450 000
C. 94 444 000
D. 94 400 000
-
Câu 13:
Tìm TXĐ của hàm số \(y = \sqrt {2 - x} + \sqrt {7 + x} \).
A. (-7; 2)
B. \(\left[ {2; + \infty } \right)\)
C. \(\left[ { - 7;2} \right]\)
D. \(R\backslash \left\{ { - 7;2} \right\}\)
-
Câu 14:
Tập xác định của hàm số \(y = \left\{ \begin{array}{l} \sqrt {3 - x} \,\,,\,\,x \in \left( { - \infty ;0} \right)\\ \sqrt {\frac{1}{x}} \,\,\,\,\,\,\,\,,\,\,x \in \left( {0; + \infty } \right) \end{array} \right.\) là tập nào dưới đây?
A. R \ {0}
B. R \ [0; 3]
C. R \ {0; 3}
D. R
-
Câu 15:
Trong các hàm số sau đây: y = |x|; \(y = {x^2} + 4x\); \(y = - {x^4} + 2{x^2}\) có bao nhiêu hàm số chẵn?
A. 0
B. 1
C. 2
D. 3
-
Câu 16:
Cho hàm số y = x - 2. Khẳng định nào sau đây là khẳng định sai?
A. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2.
B. Hàm số nghịch biến trên tập R.
C. Hàm số có tập xác định là R.
D. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -2.
-
Câu 17:
Cho hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l} {x^2} + 3x{\rm{\ khi \ }}x \ge 0\\ 1 - x{\rm{\ khi \ }}x < 0 \end{array} \right.\). Khi đó, \(f\left( 1 \right) + f\left( { - 1} \right)\) bằng bao nhiêu?
A. 2
B. -3
C. 6
D. 0
-
Câu 18:
Một hàm số bậc nhất y = f(x) có \(f\left( { - 1} \right) = 2,f\left( 2 \right) = - 3\). Hỏi hàm số đó là hàm số nào dưới đây?
A. \(y = - 2x + 3\)
B. \(y = \frac{{ - 5x - 1}}{3}\)
C. \(y = \frac{{ - 5x + 1}}{3}\)
D. \(y = 2x - 3\)
-
Câu 19:
Với những giá trị nào của m thì hàm số \(f\left( x \right) = \left( {m + 1} \right)x + 2\) đồng biến?
A. m = 0
B. m = 1
C. m < 0
D. \(m > - 1\)
-
Câu 20:
Cho hai đường thẳng
\(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) lần lượt có phương trình: \(mx + \left( {m - 1} \right)y - 2\left( {m + 2} \right) = 0\) và \(3mx - \left( {3m + 1} \right)y - 5m - 4 = 0\). Xác định vị trí tương đối của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) khi \(m = \frac{1}{3}\).A. Song song với nhau.
B. Cắt nhau tại 1 điểm.
C. Vuông góc nhau.
D. Trùng nhau.
-
Câu 21:
Cho parabol \(\left( P \right):y = a{x^2} + bx + c\) có đồ thị như hình bên. Phương trình của parabol này là phương trình nào dưới đây?
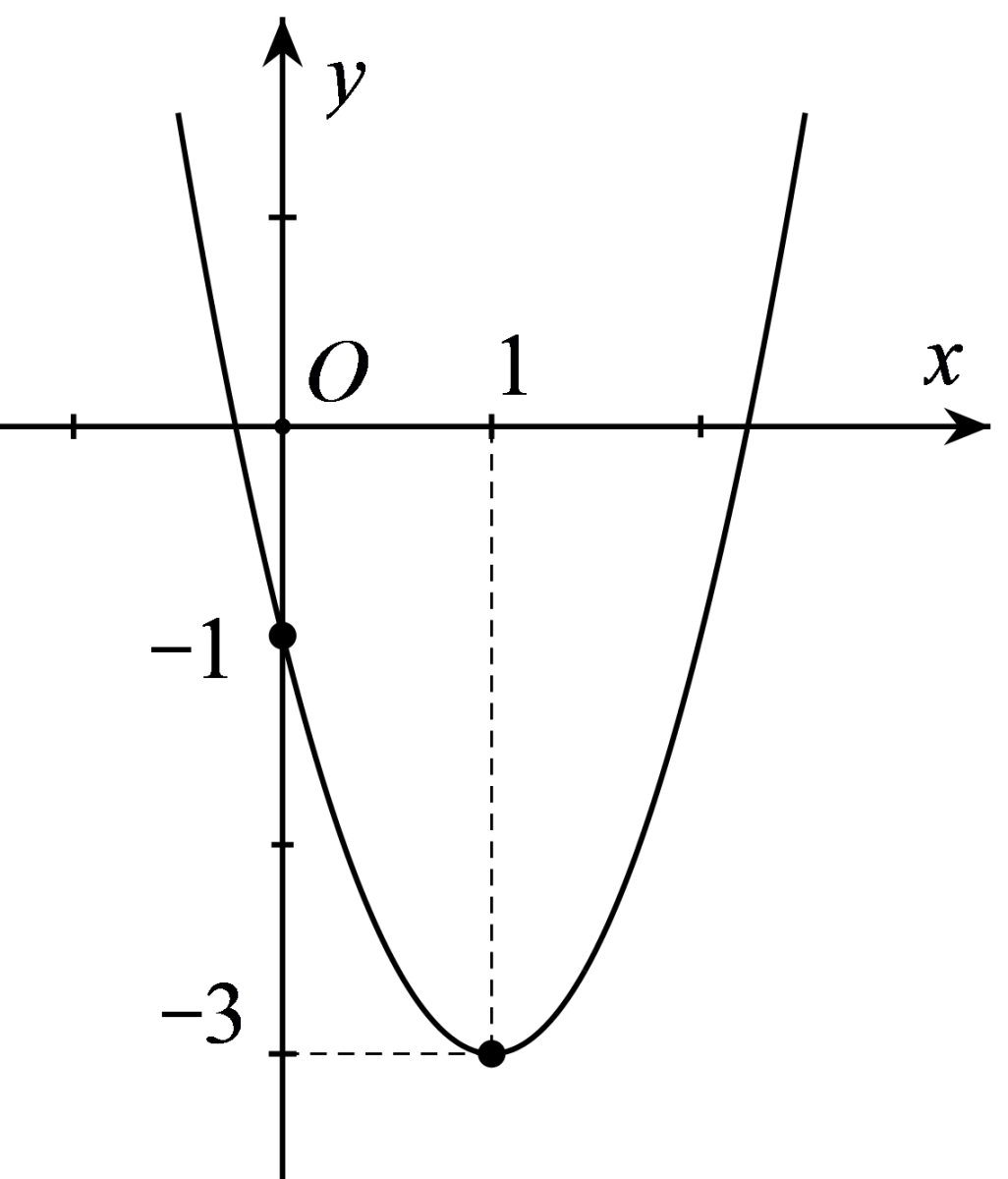
A. \(y = 2{x^2} - 4x - 1\)
B. \(y = 2{x^2} + 3x - 1\)
C. \(y = 2{x^2} + 8x - 1\)
D. \(y = 2{x^2} - x - 1\)
-
Câu 22:
Hàm số nào sau đây có giá trị nhỏ nhất tại \(x = \frac{3}{4}\)?
A. \(y = 4{x^2} - 3x + 1\)
B. \(y = - {x^2} + \frac{3}{2}x + 1\)
C. \(y = - 2{x^2} + 3x + 1\)
D. \(y = {x^2} - \frac{3}{2}x + 1\)
-
Câu 23:
Parabol \(y = a{x^2} + bx + 2\) đi qua hai điểm M(1; 5) và N(-2; 8) có phương trình là phương trình nào dưới đây?
A. \(y = {x^2} + x + 2\)
B. \(y = {x^2} + 2x\)
C. \(y = 2{x^2} + x + 2\)
D. \(y = 2{x^2} + 2x + 2\)
-
Câu 24:
Parabol \(y = a{x^2} + bx + c\) đi qua A(8;0) và có đỉnh S(6;-12) có phương trình là phương trình nào dưới đây?
A. \(y = {x^2} - 12x + 96\)
B. \(y = 2{x^2} - 24x + 96\)
C. \(y = 2{x^2} - 36x + 96\)
D. \(y = 3{x^2} - 36x + 96.\)
-
Câu 25:
Tìm giao điểm của parabol \(y = {x^2} - 3{\rm{x}} + 2\) với đường thẳng \(y = x - 1\).
A. \(\left( {1;0} \right),{\rm{ }}\left( {3;2} \right).\)
B. \(\left( {0; - 1} \right),\left( { - 2; - 3} \right).\)
C. (-1; 2); (2;1)
D. (2; 1); (0; -1)
-
Câu 26:
Trong bốn phép biến đổi sau, phép biến đổi nào là phép biến đổi tương đương?
A. \(\frac{{x\left( {x - 1} \right)}}{{x - 1}} = 1 \Leftrightarrow x = 1\)
B. \(\left| x \right| = 2 \Leftrightarrow x = 2\)
C. \(x + \sqrt {x - 4} = 3 + \sqrt {x - 4} \Leftrightarrow x = 3\)
D. \(x - \sqrt {x - 5} = 3 \Leftrightarrow x - 3 = \sqrt {x - 5} \)
-
Câu 27:
Nghiệm của phương trình \(\frac{{x + 2}}{x} = \frac{{2x + 3}}{{2x - 4}}\) là giá trị nào dưới đây?
A. \(x = - \frac{3}{8}\)
B. \(x = \frac{3}{8}\)
C. \(x = \frac{8}{3}\)
D. \(x = - \frac{8}{3}\)
-
Câu 28:
Tìm tất cả các giá trị của m để phương trình \({m^2}\left( {x + m} \right) = x + m\) có vô số nghiệm?
A. \(m = \pm1\)
B. m = 0 hoặc m = 1
C. m = 0 hoặc m = -1
D. \( - 1 < m < 1,\,m \ne 0\)
-
Câu 29:
Cho phương trình \(\frac{1}{4}{x^2} - \left( {m - 3} \right)x + {m^2} - 2m + 7 = 0\).Tìm m để phương trình có hai nghiệm phân biệt.
A. \(m \ge \frac{1}{2}\)
B. \(m < - \frac{1}{2}\)
C. \(m > \frac{1}{2}\)
D. \(m < \frac{1}{2}\)
-
Câu 30:
Cho phương trình \({x^2} - 2(m - 1)x + {m^2} - 3m + 4 = 0\).Tìm m để phương trình có 2 nghiệm phân biệt \({x_1},{x_2}\) thỏa \(x_1^2 + x_2^2 = 20\).
A. \(m = - 3,m = 4\)
B. m = 4
C. m = -3
D. \(m = 3,m = - 4\)
-
Câu 31:
Biết \(\cos \alpha = \frac{1}{3}\). Giá trị đúng của biểu thức \(P = {\sin ^2}\alpha + 3{\cos ^2}\alpha \) bằng bao nhiêu?
A. \(\dfrac13\)
B. \(\dfrac{{10}}{9}\)
C. \(\dfrac{{11}}{9}\)
D. \(\dfrac{{4}}{3}\)
-
Câu 32:
Cho \(\alpha \) là góc tù. Điều khẳng định nào sau đây là đúng?
A. \(\sin \alpha < 0\)
B. \(\cos \alpha > 0\)
C. \(\tan \alpha < 0\)
D. \(\cot \alpha > 0\)
-
Câu 33:
Cho hình chữ nhật ABCD có \(AB = \sqrt 2 ,\) AD = 1. Tính góc giữa hai vec tơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} .\)
A. 89o
B. 92o
C. 109o
D. 91o
-
Câu 34:
Cho đoạn thẳng AB = 4, AC = 3, \(\overrightarrow {AB} .\overrightarrow {AC} = k\). Hỏi có mấy điểm C để k = -12?
A. 2
B. 0
C. 1
D. 3
-
Câu 35:
Cho tam giác ABC có H là trực tâm. Biểu thức \({\left( {\overrightarrow {AB} + \overrightarrow {HC} } \right)^2}\) bằng biểu thức nào sau đây?
A. \(A{B^2} + H{C^2}\)
B. \({\left( {AB + HC} \right)^2}\)
C. \(A{C^2} + A{H^2}\)
D. \(A{C^2} + 2A{H^2}.\)
-
Câu 36:
Nếu tam giác ABC là tam giác đều thì mệnh đề nào sau đây đúng ?
A. \(\overrightarrow {AB.} \overrightarrow {AC} = \frac{1}{2}A{B^2}\)
B. \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{\sqrt 3 }}{2}A{B^2}\)
C. \(\overrightarrow {AB.} \overrightarrow {AC} = \frac{1}{4}A{B^2}\)
D. \(\overrightarrow {AB.} \overrightarrow {AC} = 0.\)
-
Câu 37:
Cho 2 vectơ \(\overrightarrow u = (4;5)\) và \(\overrightarrow v = (3;a)\). Tính a để \(\overrightarrow u .\overrightarrow v = 0\).
A. \(a = \frac{{12}}{5}\)
B. \(a =- \frac{{12}}{5}\)
C. \(a = \frac{5}{{12}}\)
D. \(a =- \frac{5}{{12}}\)
-
Câu 38:
Trong mặt phẳng \(\left( {O,\overrightarrow i ,\overrightarrow j } \right)\) cho ba điểm \(A\left( {3;6} \right),{\rm{ }}B\left( {x; - 2} \right),{\rm{ }}C\left( {2;y} \right).\theta \). Tính \(\overrightarrow {OA} .\overrightarrow {BC} .\)
A. \(\overrightarrow {OA} .\overrightarrow {BC} = 3x + 6y - 12\)
B. \(\overrightarrow {OA} .\overrightarrow {BC} = - 3x + 6y + 18\)
C. \(\overrightarrow {OA} .\overrightarrow {BC} = - 3x + 6y + 12\)
D. \(\overrightarrow {OA} .\overrightarrow {BC} = 0\)
-
Câu 39:
Cho các vectơ \(\vec a = \left( {1; - 2} \right)\), \(\vec b = \left( { - 2; - 6} \right)\). Khi đó góc giữa chúng là bao nhiêu?
A. 45o
B. 60o
C. 30o
D. 135o
-
Câu 40:
Cho hai điểm M(1;-2) và N(-3;4). Khoảng cách giữa hai điểm M và N bằng bao nhiêu?
A. 4
B. 6
C. \(3\sqrt 6 \)
D. \(2\sqrt {13} \)
