Đề thi giữa HK2 môn Toán 9 năm 2021
Trường THCS Nguyễn Đình Chiểu
-
Câu 1:
Cho đường thẳng d có phương trình (m - 2)x + (3m - 1)y = 6m - 2. Tìm các giá trị của tham số m để d đi qua gốc tọa độ.
A. 1/3
B. 2/3
C. 2
D. 3
-
Câu 2:
Cho đường thẳng d có phương trình \( \frac{{m - 1}}{2}x + (1 - 2m)y = 2\) Tìm các giá trị của tham số m để d song song với trục tung.
A. 1
B. 2
C. 3
D. 1/2
-
Câu 3:
Cho đường thẳng d có phương trình (m - 2)x + (3m - 1)y = 6m + 2 Tìm các giá trị của tham số m để d song song với trục tung.
A. 1/3
B. 2
C. 2/3
D. 3
-
Câu 4:
Cho đường thẳng d có phương trình (5m - 15)x + 2my = m - 2 Tìm các giá trị của tham số m để d song song với trục hoành.
A. 1
B. 2
C. 3
D. 4
-
Câu 5:
Cho đường thẳng d có phương trình (m - 2)x + (3m - 1)y = 6m - 2 Tìm các giá trị của tham số m để d song song với trục hoành.
A. 1
B. 2
C. 3
D. 4
-
Câu 6:
Đường thẳng nào sau đây không song song với đường thẳng y = 7x + 3?
A. y = 7x
B. y = 4 - 7x
C. y = 7x + 1
D. y = - 1 + 7x
-
Câu 7:
Cho hệ phương trình \(\left\{ \begin{array}{l} y = ( - 2 - m)x + 2\\ y = (m + 4)x + 19 \end{array} \right.\). Tìm m để hệ phương trình trên có nghiệm duy nhất?
A. m = 3
B. m = -3
C. m ≠ -3
D. m ≠ 3
-
Câu 8:
Cho hệ phương trình \(\left\{ \begin{array}{l} y = 2{\rm{x}} + 20\\ y = (2m - 4)x + 10 \end{array} \right.\). Tìm m để hệ phương trình đã cho vô nghiệm
A. m = 3
B. m = 1
C. m = -2
D. m = -1
-
Câu 9:
Không vẽ hình, hỏi hệ phương trình sau có bao nhiêu nghiệm: \(\left\{ \begin{array}{l} - 2{\rm{x}} + 5y = 10\\ 16{\rm{x}} - 40y = 20 \end{array} \right.\)
A. Vô số nghiệm
B. 0
C. 1
D. 2
-
Câu 10:
Không vẽ hình, hãy cho biết hệ phương trình sau có bao nhiêu nghiệm?
A. 1
B. Vô số
C. 0
D. 2
-
Câu 11:
Tìm giá trị của m để x = 4 thỏa mãn hệ phương trình sau: \(\left\{ \begin{array}{l}5x - 10y = 50\\mx + 10y = 6\end{array} \right.\)
A. m = 7
B. m = 8
C. m = 9
D. m = 10
-
Câu 12:
Giải hệ phương trình \(\left\{ \begin{array}{l}\dfrac{{2x}}{3} - \dfrac{{5y}}{3} = 1\\4x - 10y = 6\end{array} \right.\)
A. Vô nghiệm
B. Vô số nghiệm
C. (1;2)
D. (-3;2)
-
Câu 13:
Gọi (a;b) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + y\sqrt 3 = 0\\x\sqrt 3 + 2y = 2\end{array} \right.\).Tính a2 + b
A. 6
B. 8
C. 10
D. 12
-
Câu 14:
Số nghiệm của hệ phương trình \(\left\{ \begin{array}{l}\dfrac{x}{2} - \dfrac{y}{3} = 1\\3x - 2y = 6\end{array} \right.\)
A. 0
B. 1
C. 2
D. Vô số nghiệm
-
Câu 15:
Hệ phương trình \(\left\{ \begin{array}{l}2x + 5y = 1\\6x - 15y = 4\end{array} \right.\) có bao nhiêu nghiệm?
A. 0
B. 1
C. 2
D. Vô số
-
Câu 16:
Hệ phương trình \(\left\{ \begin{array}{l}4x + 3y = 6\\2x + y = 4\end{array} \right.\) có nghiệm là:
A. \(\left( {x;y} \right) = \left( {3; 2} \right)\)
B. \(\left( {x;y} \right) = \left( {3; - 2} \right)\)
C. \(\left( {x;y} \right) = \left( {-3; - 2} \right)\)
D. \(\left( {x;y} \right) = \left( {-3; 2} \right)\)
-
Câu 17:
Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x + 5y = 8\\2x - 3y = 0\end{array} \right.\) là:
A. \(\left( {x;y} \right) = \left( {-\dfrac{3}{2};-1} \right)\)
B. \(\left( {x;y} \right) = \left( {\dfrac{3}{2};-1} \right)\)
C. \(\left( {x;y} \right) = \left( {-\dfrac{3}{2};1} \right)\)
D. \(\left( {x;y} \right) = \left( {\dfrac{3}{2};1} \right)\)
-
Câu 18:
Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}3x + y = 3\\2x - y = 7\end{array} \right.\) là:
A. \(\left( {x;y} \right) = \left( {2; - 3} \right)\)
B. \(\left( {x;y} \right) = \left( {-2; - 3} \right)\)
C. \(\left( {x;y} \right) = \left( {2; 3} \right)\)
D. \(\left( {x;y} \right) = \left( {2; - 3} \right)\)
-
Câu 19:
Cho \(\left\{ \begin{array}{l}\left( {1 + \sqrt 3 } \right)x + \left( {\sqrt 2 - 1} \right)y = 1\\\left( {1 + \sqrt 2 } \right)x + \left( {1 - \sqrt 3 } \right)y = 1\end{array} \right.\) có nghiệm là (a;b). Tính 3a + 3b.
A. \(2\sqrt2+1\)
B. \(2\sqrt2-1\)
C. \(2\sqrt2-2\)
D. \(2\sqrt2+2\)
-
Câu 20:
Cho \(\left\{ \begin{array}{l}\dfrac{2}{3}x - y = 70\\\dfrac{1}{3}x - \dfrac{2}{3}y = 43\end{array} \right.\) có nghiệm nào dưới đây?
A. (33; 48)
B. (33; - 48)
C. (- 33; - 48)
D. (- 33; 48)
-
Câu 21:
Hai anh An và Đông cùng nhau lát gạch sàn phòng truyền thống của trường trong 7 giờ 12 phút thì xong. Nếu từ đầu, anh An chỉ làm trong 4 giờ, anh Đông làm tiếp trong 3 giờ nữa thì chỉ lát được 50 % diện tích sàn. Hỏi nếu chỉ làm một mình thì mỗi anh lát xong sàn truyền thống trong thời gian bao lâu?
A. Anh An: 11h Anh Đông: 19h
B. Anh An: 19h Anh Đông: 11h
C. Anh An: 18h Anh Đông: 12h
D. Anh An: 12h Anh Đông: 18h
-
Câu 22:
Một hình chữ nhật có chu vi 110 m. Biết rằng hai lần chiều dài hơn ba lần chiều rộng là 10 m. Tính diện tích hình chữ nhật.
A. 700m2
B. 600m2
C. 500m2
D. 800m2
-
Câu 23:
Bạn Linh đợi mẹ ở cổng trường. Khi gặp mẹ, Linh sực nhớ đến để quên cuốn sách Tài liệu Dạy – Học Toán 9 tập 2 ở trên lớp nên di chuyển từ cổng trường vào lớp trên quãng đường dài 60m, lấy sách rồi quay trở ra cổng trường gặp mẹ. Biết tốc độ khi đi vào nhanh hơn tốc độ khi ra là 0,5 m/giây và thời gian lúc chạy vào ngắn hơn lúc đi ra là 20 giây. Hãy tìm tốc độ lúc đi ra của bạn Linh.
A. 2m/s
B. 0,5m/s
C. 1,5m/s
D. 1m/s
-
Câu 24:
Cuối học kì 1, số học sinh giỏi của lớp 9A bằng 20% số học sinh cả lớp. Đến cuối học kì 2, lớp có thêm 2 bạn đạt học sinh giỏi nên số học sinh giỏi bằng \(\dfrac{1}{4}\) số học sinh của lớp. Hỏi lớp 9A có bao nhiêu học sinh ?
A. 35 hs
B. 40 hs
C. 45 hs
D. 50 hs
-
Câu 25:
Một trường học tổ chức cho 160 người tham gia du lịch sinh thái. Vé cho mỗi giáo viên phụ trách lớp là 30000 đồng và vé cho mỗi học sinh là 20000 đồng. Tổng số tiền mua vé là 3 300000 đồng. Hỏi có bao nhiêu giáo viên và bao nhiêu học sinh tham gia ?
A. 5 giáo viên; 155 học sinh
B. 10 giáo viên; 150 học sinh
C. 20 giáo viên; 140 học sinh
D. 15 giáo viên; 145 học sinh
-
Câu 26:
Cho đường tròn (O;R) có hai dây cung AB và CD vuông góc với nhau tại I ( C thuộc cung nhỏ AB ). Kẻ đường kính BE của (O). Đẳng thức nào sau đây là sai?
A. \(I{A^2} + I{C^2} + I{B^2} + I{D^2} = A{D^2} + B{C^2}\)
B. \(I{A^2} + I{C^2} + I{B^2} + I{D^2} = B{D^2} + A{C^2}\)
C. \(I{A^2} + I{C^2} + I{B^2} + I{D^2} = B{E^2}\)
D. \(I{A^2} + I{C^2} + I{B^2} + I{D^2} = A{D^2}\)
-
Câu 27:
Cho đường tròn (O;R), dây cung \(AB=R\sqrt3\). Vẽ đường kính CD vuông góc AB (C thuộc cung lớn AB). Trên cung AC nhỏ lấy điểm M, vẽ dây AN//CM. Độ dài đoạn MN là
A. \(MN=R\sqrt3\)
B. \(MN=R\sqrt2\)
C. \(MN = \frac{{3R }}{2}\)
D. \(MN = \frac{{R\sqrt 5 }}{2}\)
-
Câu 28:
Cho tam giác ABC có góc B = 300 , đường trung tuyến AM, đường cao CH. Vẽ đường tròn ngoại tiếp BHM. Kết luận nào sai khi nói về các cung HB;MB;MH của đường tròn ngoại tiếp tam giác MHB ?
A. Cung HB lớn nhất
B. Cung HB nhỏ nhất
C. Cung MH nhỏ nhất
D. Cung MB=MB= cung MH
-
Câu 29:
Cho tam giác ABC có góc B = 600 , đường trung tuyến AM, đường cao CH. Vẽ đường tròn ngoại tiếp BHM. Kết luận nào đúng khi nói về các cung HB;MB;MH của đường tròn ngoại tiếp tam giác MHB
A. Cung HB nhỏ nhất
B. Cung MB lớn nhất
C. Cung MH nhỏ nhất
D. Ba cung bằng nhau
-
Câu 30:
Cho đường tròn (O;R) có hai dây cung AB và CD vuông góc với nhau tại I ( C thuộc cung nhỏ AB ). Kẻ đường kính BE của (O). Đẳng thức nào sau đây là đúng?
A. \(I{A^2} + I{C^2} + I{B^2} + I{D^2} = 2{R^2}\)
B. \(I{A^2} + I{C^2} + I{B^2} + I{D^2} = 3{R^2}\)
C. \(I{A^2} + I{C^2} + I{B^2} + I{D^2} =4{R^2}\)
D. \(I{A^2} + I{C^2} + I{B^2} + I{D^2} = 5{R^2}\)
-
Câu 31:
Góc nội tiếp chắn nửa đường tròn bằng bao nhiêu độ?
A. 450
B. 600
C. 900
D. 1200
-
Câu 32:
Khẳng định nào sau đây là sai?
A. Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông
B. Trong một đường tròn, hai góc nội tiếp bằng nhau chắn hai cung bằng nhau
C. Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau
D. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung.
-
Câu 33:
Góc nội tiếp có số đo
A. Bằng hai lần số đo góc ở tâm cùng chắn một cung
B. Bằng nửa số đo cung bị chắn.
C. Bằng số đo cung bị chắn
D. Bằng số đo của góc ở tâm cùng chắn một cung
-
Câu 34:
Góc nội tiếp nhỏ hơn hoặc bằng 900 có số đo
A. Bằng nửa số đo góc ở tâm cùng chắn một cung
B. Bằng số đo của góc ở tâm cùng chắn một cung
C. Bằng số đo cung bị chắn
D. Bằng nửa số đo cung lớn.
-
Câu 35:
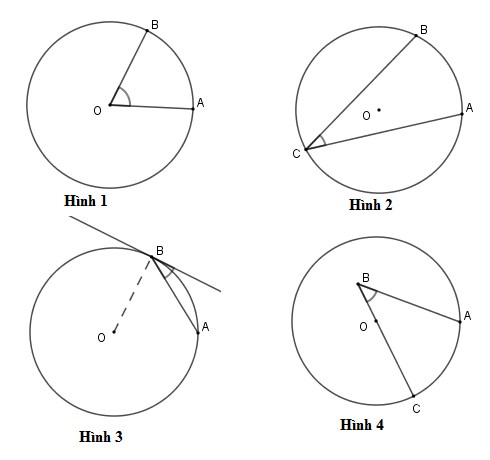
Hình nào dưới đây biểu diễn góc nội tiếp?
A. Hình 2
B. Hình 1
C. Hình 3
D. Hình 4
-
Câu 36:
Cho (O;R) có hai đường kính AB,CD vuông góc với nhau. Gọi M là điểm chính giữa cung BC. Dây AM cắt OC tại E , dây CM cắt đường thẳng AB tại N. Tam giác MCE là tam giác gì?
A. ΔMEC đều
B. ΔMEC cân tại E
C. ΔMEC cân tại M
D. ΔMEC cân tại C
-
Câu 37:
Trên (O ) lấy bốn điểm A,B,C,D theo thứ tự sao cho cung AB = cung BC = cung CD. Gọi I là giao điểm của BD và AC , biết góc BIC = 800. Tính góc ACD
A. 200
B. 150
C. 350
D. 300
-
Câu 38:
Cho đường tròn (O) và điểm E nằm ngoài đường tròn. Vẽ cát tuyến EAB và ECD với đường tròn A nằm giữa E và B, C nằm giữa E và D. Gọi F là một điểm trên đường tròn sao cho B nằm chính giữa cung DF, I là giao điểm của FA và BC. Biết góc E = 250, số đo góc AIC là:
A. 200
B. 500
C. 250
D. 300
-
Câu 39:
Cho nửa đường tròn (O) đường kính AB và C là điểm trên cung nhỏ AB (cung CB nhỏ hơn cung CA). Tiếp tuyến tại C của nửa đường tròn cắt đường thẳng AB tại D . Biết tam giác ADC cân tại C. Tính góc ADC
A. 400
B. 450
C. 600
D. 300
-
Câu 40:
Trên (O) lấy bốn điểm A,B,C,D theo thứ tự sao cho cung AB = cung BC = cung CD . Gọi I là giao điểm của BD và AC, biết góc BIC) = 700 . Tính góc ABD
A. 200
B. 150
C. 350
D. 300