Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB, CD. Gọi d là giao tuyến của hai mặt phẳng (SAD) và mặt phẳng (SBC). Trong các đường thẳng AD, MN, CB, AC, BD, đường thẳng d song song với bao nhiêu đường thẳng?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai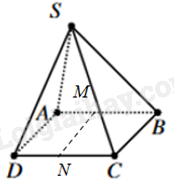
Vì ABCD là hình bình hành nên AD//CB
Mà \(AD \subset mp\left( {SAD} \right),CB \subset mp\left( {SCB} \right)\) và S thuộc cả hai mặt phẳng (SAD) và (SCB) nên giao tuyến d của hai mặt phẳng (SAD) và (SCB) là một đường thẳng song song đi qua S và song song với AD, CB.
Lại có, M, N lần lượt là trung điểm của AB, CD trong hình bình hành ABCD nên MN//AD//BC. Suy ra: d// MN//AD//BC
Vậy đường thẳng d song song với 3 đường thẳng là: MN, AD, BC.
Đáp án C
Đề thi giữa HK1 môn Toán 11 CD năm 2023-2024
Trường THPT Trần Nhân Tông