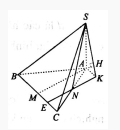
Cho hình chóp SABC, đáy ABC là tam giác đều cạnh a, SA vuông góc với đáy và SA = a. Gọi M, N lần lượt là trung điểm của các cạnh BC và CA. Khoảng cách giữa hai đường thẳng AM và SN bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Gọi E là trung điểm của MC. Qua A kẻ một đường thẳng song song với BC cắt đường thẳng NE tại K. Kẻ AH⊥SK (H∈SK). Ta có AM // KE ⇒AM// (SKE). Do đó d(AM,SN)=d(A,(SKE)). Ta dễ chứng minh được AH⊥(SKE) nên d(A,(SKE))=AH. Tam giác SAK vuông ở A và có AH là đường cao nên\( \frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{K^2}}} = \frac{1}{{{a^2}}} + \frac{{16}}{{{a^2}}} = \frac{{17}}{{{a^2}}} \to AH = \frac{a}{{\sqrt {17} }}\)
Câu hỏi liên quan
-
Cho hình lập phương \(ABCD.A'B'C'D'\). I là trung điểm BB’. Mặt phẳng (DIC’) chia khối lập phương thành 2 phần có tỉ số thể tích phần bé chia phần lớn bằng:
-
Cho hình chóp S.ABC có SB vuông góc với mặt phẳng (ABC), đáy ABC là tam giác vuông cân đỉnh B, cạnh huyền AC = \(a\sqrt 2 \), mặt bên (SAC) hợp với đáy một góc 600. Tính thể tích khối chóp S.ABC.
-
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại C, \(AB = a\sqrt 5 \), AC = a. Cạnh bên SA = 3a và vuông góc với mặt phẳng \(\left( {ABC} \right)\). Tính thể tích khối chóp S.ABC.
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Biết \(SA \bot (ABCD);\,\,SA = a\sqrt 3 .\) Tính thể tích của khối chóp.
-
Cho hình chóp S ABC . có đáy là tam giác vuông cân tại C, AB = 3. Hình chiếu vuông góc của S xuống mặt đáy trùng với trọng tâm của tam giác ABC và \(S B=\frac{\sqrt{14}}{2}\). Thể tích của khối chóp đã cho bằng
-
Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên với mặt đáy bằng 600 .Thể tích của khối chóp đã cho bằng
-
Cho hình chóp \(S.ABCD\) có đáy ABCD là hình vuông cạnh a, hai mặt phẳng \(\left( SAB \right)\) và \(\left( SAD \right)\) cùng vuông góc với mặt phẳng \(\left( ABCD \right)\); góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( ABCD \right)\) bằng \(60{}^\circ \). Tính theo a thể tích khối chóp \(S.ABCD\).
-
Cho khối tự diện OABC có OA, OB, OC đôi một vuông góc và OA = a; OB = b; OC = c. Thể tích khối tứ diện OABC được tính theo công thức nào sau đây
-
Cho hình chóp S.ABC có \( SA = SB = SC = a\sqrt 3 ;AB = AC = a;BC = 3a\). Thể tích khối chóp S.ABC bằng:
-
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, BC = 2a, SA = 2a, SA vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD theo a.
-
Cho khối chóp S.ABC. Trên các đoạn SA, SB, SC lần lượt lấy ba điểm A', B', C’ sao cho \(SA'=\frac{1}{2}SA;SB'=\frac{1}{3}SB;SC'=\frac{1}{4}SC\). Khi đó tỉ số thể tích của hai khối chóp S.A'B'C' và S.ABC bằng:
-
Cho khối hộp \(ABCD.A'B'C'D'\) có cạnh bên bằng 1; đáy \(ABCD\) là một hình chữ nhật có các cạnh \(BA=\sqrt{3},AD=\sqrt{7};\) các mặt bên \(\left( ABB'A' \right)\) và \(\left( ADD'A' \right)\) hợp với mặt đáy các góc theo thứ tự \({{45}^{0}};{{60}^{0}}.\) Thể tích khối hộp là:
-
Một hồ bơi hình hộp chữ nhật có đáy là hình vuông cạnh 50m. Lượng nước trong hồ cao 1,5m. Vậy thể tích nước trong hồ là:
-
Một quả bóng có bán kính \(10\left( {cm} \right)\) được đặt khít vào một hộp cứng dạng hình hộp. Tính thể tích khối hộp đó.
-
Tính thể tích V của khối lập phương \(ABCD.{A_1}{B_1}C{}_1{D_1}\), biết diện tích mặt chéo \(AC{C_1}{A_1}\) bằng \(4\sqrt 2 {a^2}\)
-
Cho hình chóp S.ABC có tam giác SBC là tam giác vuông cân tại S, S B=2 a và khoảng cách từ A đến mặt phẳng (SBC) bằng 3a. Thể tích khối chóp đã cho bằng
-
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh A và AB = AC, SA = SB = SC = 3a. Góc giữa mặt phẳng (SAB) và mặt phẳng (ABC) là 60o. Gọi G là trọng tâm của tam giác SAB. Thể tích khối chóp S.GBC là:
-
Thể tích của khối có 5 mặt hình chữ nhật, 4 mặt tam giác với kích thước được cho như hình vẽ là
.png)
-
Cho hình lăng trụ \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có đáy là tam giác đều cạnh \(2 a \sqrt{2}\) và \(A^{\prime} A=a \sqrt{3}\). Hình chiếu vuông góc của điểm A' trên mặt phẳng (ABC) trùng với trọng tâm G của tam giác ABC. Thể tích của khối lăng trụ đã cho bằng
-
Cho hình lập phương \(ABCD.ABCD\). Mặt phẳng (BDC’) chia khối lập phương thành 2 phần có tỉ lệ thể tích phần nhỏ so với phần lớn là :
