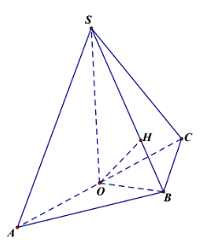
Cho hình chóp S.ABC, đáy là tam giác ABC có AB=BC√5,AC=2BC√2AB=BC√5,AC=2BC√2, hình chiếu của S lên mặt phẳng (ABC) là trung điểm O của cạnh AC. Khoảng cách từ A đến mặt phẳng (SBC) bằng 2. Mặt phẳng (SBC) hợp với mặt phẳng (ABC) một góc (alpha ) thay đổi. Biết rằng giá trị nhỏ nhất của thể tích khối chóp S.ABC bằng √ab√ab, trong đó (a,b thuộc N*), a là số nguyên tố. Tổng a + b bằng:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi H là hình chiếu của O lên SB.
Ta có: OB=√2BC2+2BA2−AC24=BC;OC=12AC=BC√2OB=√2BC2+2BA2−AC24=BC;OC=12AC=BC√2. Suy ra OB⊥BC
Dễ thấy ∠SBO=α∠SBO=α và OH=d(O;(SBC))=12d(A;(SBC))=1OH=d(O;(SBC))=12d(A;(SBC))=1
Suy ra
SO=OHcosα=1cosα;OB=OHsinα=1sinα⇒BC=OB=1sinα
Thể tích khối chóp S.ABC là:
VS.ABC=13SO.SABC=13SO.2SOBC=13.1cosα.(1sinα)2=13cosα.sin2α
Áp dụng bất đẳng thức Cô-si ta có:
1=12sin2α+12sin2α+cos2α≥3.3√14sin4α.cos2α⇔127≥14.sin4α.cos2α⇒1sin2αcos2α≥3√32⇒VS.ABC≥√32
VậyminVS.ABC=√32. Dấu “=” xảy ra
⇔cos2α=12sin2α=13⇔cosα=√33⇒a=3,b=2
Vậy a+b=3+2=5
Đáp án cần chọn là: B