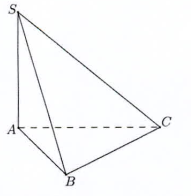
Cho hình chóp S.ABC biết \(AB = 8,\,\,BC = 4,\widehat {\,ABC} = {60^0}\). Hình chiếu của S lên cạnh AB là điểm K sao cho KB = 3KA. Biết \(SB,\,SC\) cùng hợp với đáy một góc \({60^0}\). Tính thể tích khối chóp S.ABC.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Ta có: \(AC = \sqrt {A{B^2} + B{C^2} – 2AB.BC.\cos \widehat {ABC}} = 4\sqrt 3 \).
Trong \(\Delta ABC\) có: \(A{B^2} = B{C^2} + A{C^2}\) nên \(\Delta ABC\) vuông tại C.
Gọi M là trung điểm của BC, H là hình chiếu vuông góc của S lên mặt phẳng \(\left( {ABC} \right)\).
Ta có: \(\left\{ \begin{array}{l}AB \bot SH\\AB \bot SK\end{array} \right. \Rightarrow AB \bot HK\).
Ta có BH là hình chiếu của SB trên mp \(\left( {ABC} \right)\), CH là hình chiếu của SC trên mp \(\left( {ABC} \right)\) nên góc giữa SB và mp \(\left( {ABC} \right)\) là góc \(\widehat {SBH}\) và góc giữa SC và mp \(\left( {ABC} \right)\) là góc \(\widehat {SCH}\). Theo giả thiết: \(\widehat {SBH} = \widehat {SCH} = {60^0}\) do đó: \(HB = HC \Rightarrow HM \bot BC \Rightarrow HM//AC\).
Suy ra đường thẳng HM đi qua trung điểm I của AB.
Ta có \(\Delta HKI\) và \(\Delta BMI\) đồng dạng nên: \(\frac{{HI}}{{BI}} = \frac{{KI}}{{MI}} \Leftrightarrow \frac{{HI}}{4} = \frac{2}{{2\sqrt 3 }} \Leftrightarrow HI = \frac{{4\sqrt 3 }}{3}\).
Do đó \(HM = HI + IM = \frac{{4\sqrt 3 }}{3} + 2\sqrt 3 = \frac{{10\sqrt 3 }}{3}, HB = \sqrt {H{M^2} + M{B^2}} = \sqrt {{{\left( {\frac{{10\sqrt 3 }}{3}} \right)}^2} + 4} = \frac{{4\sqrt {21} }}{3}\),
\(SH = HB.tan{60^0} = 4\sqrt 7 \).
Diện tích tam giác ABC: \({S_{ABC}} = \frac{1}{2}AC.BC = 8\sqrt 3 \).
Thể tích khối chóp S.ABC là \(V = \frac{1}{3}SH.{S_{ABC}} = \frac{1}{3}4\sqrt 7 .8\sqrt 3 = \frac{{32\sqrt {21} }}{3}\).
Câu hỏi liên quan
-
Tính diện tích toàn phần S của hình chóp có đáy là hình vuông diện tích bằng 4 và các mặt bên là các tam giác đều.
-
Tính thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh bằng a.
-
Cho khối lăng trụ có thể tích bằng 58 cm³ và diện tích đáy bằng 16 cm². Chiều cao của lăng trụ là:
-
Cho hình chóp \(S.ABCD\) có đáy ABCD là hình chữ nhật, tam giác \(SAD\) vuông tại \(S\) và nằm trong mặt phẳng vuông góc với đáy. Cho biết AB=a, \(SA=2SD\). Mặt phẳng \(\left( SBC \right)\) tạo với đáy một góc \({{60}^{\text{o}}}\). Thể tích khối chóp \(S.ABCD\) là
-
Cho hình chóp S.ABC có đáy là tam giác vuông tại C, \(AB = a\sqrt 5 \), AC = a. Cạnh bên SA = 3a và vuông góc với mặt phẳng \(\left( {ABC} \right)\). Thể tích khối chóp S.ABC bằng:
-
Trong các mệnh đề sau đây, mệnh đề nào đúng?
-
Thể tích của khối lập phương cạnh 2a bằng
-
Cho một tấm nhôm hình chữ nhật ABCD có \(AD=60cm\). Ta gấp tấm nhôm theo 2 cạnh MN và PQ vào phía trong đến khi AB và DC trùng nhau như hình vẽ dưới đây để được một hình lăng trụ khuyết 2 đáy. Tìm x để thể tích khối lăng trụ lớn nhất?
.png)
-
Cho lăng trụ \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với tâm O của đường tròn ngoại tiếp tam giác ABC, biết \(A^{\prime} O=a\) . Thể tích của khối lăng trụ đã cho bằng
-
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a và đường thẳng A’C tạo với mặt phẳng (ABB’A’) một góc 300. Tính thể tích V của khối lăng trụ ABC.A’B’C’.
-
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, góc BAD = 450, tam giác SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích của hình chóp S.ABCD là:
-
Cho khối chóp S.ABC có SA vuông góc với (ABC), đáy ABC là tam giác vuông cân tại A, BC = 2a , góc giữa $SB$ và (ABC) là \({30^0}\). Tính thể tích khối chóp S.ABC.
-
Cho khối chóp có đáy là hình vuông cạnh \(a\sqrt 2 \) và chiều cao 3a. Thể tích V của khối chóp đã cho bằng:
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Tam giác SAB vuông tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Hình chiếu vuông góc của S trên AB là điểm H thỏa \(A H=2 B H\) . Thể tích của khối chóp đã cho bằng
-
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(2a\), cạnh \(SB\) vuông góc với đáy và mặt phẳng \(\left( SAD \right)\) tạo với đáy một góc \({{60}^{{}^\circ }}\). Tính thể tích khối chóp \(S.ABCD\).
-
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B , AD = 2a, AB = BC = a,SA vuông góc với đáy, SB tạo với đáy một góc 30o. Tính tỉ số thể tích \(\frac{{{V_{SABD}}}}{{{V_{SBCD}}}}?\)
-
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh B, AB = 4,SA = SB = SC = 12 . Gọi M, N, E lần lượt là trung điểm AC, BC, AB. Trên cạnh SB lấy điểm F sao cho \( \frac{{BF}}{{BS}} = \frac{2}{3}\) Thể tích khối tứ diện (MNEF ) bằng
-
Cho lăng trụ đứng \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có đáy ABC là tam giác với \(AB=a, A C=2 a, \widehat{B A C}=120^{\circ} \text { và } A A^{\prime}=2 a \sqrt{5}\). Thể tích của khối lăng trụ đã cho bằng
-
Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông tại B, \(AB=a, BC=2a\). Tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với đáy. Gọi \(G\) là trọng tâm tam giác \(ABC\), mặt phẳng \(\left( SAG \right)\) tạo với đáy một góc \(60{}^\circ \). Thể tích khối tứ diện \(ACGS\) bằng
-
Cho khối lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt thuộc các cạnh bên AA’, CC’ sao cho \(MA=MA'\) và \(NC=4NC'\). Gọi G là trọng tâm tam giác ABC. Trong bốn khối tứ diện GA’B’C’, BB’MN, ABB’C’ và A’BCN, khối tứ diện nào có thể tích nhỏ nhất?
