ADMICRO
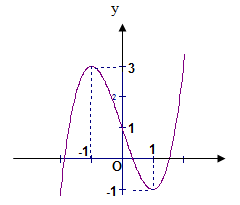
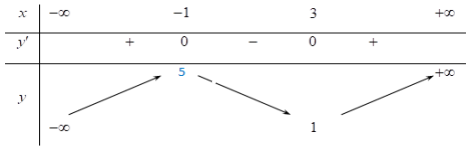
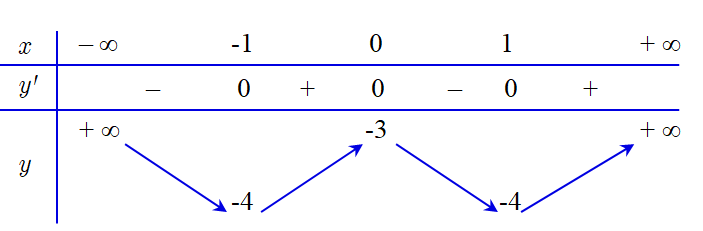
Cho hàm số y=x3+3x2−9. Tìm m để đồ thị hàm số y=|f(x)+m| có ba điểm cực tiểu.
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Môn: Toán Lớp 12
Bài: Cực trị của hàm số
ZUNIA12
Lời giải:
Báo saiĐặt F(x)=f(x)+m . Đặt {yct=−5+mycd=−9+m.
Xét hàm số y=|F(x)|={F(x) khi F(x)≥0−F(x) khi F(x)<0
Để hàm số có 3 điểm cực tiểu thì {ycd>0yct<0⇔{−5+m>0−9+m<0⇔5<m<9
ZUNIA9
AANETWORK



.jpg.png)