Đề thi thử Tốt nghiệp THPT năm 2025 môn Vật lí cụm trường miền Trung - Đề 5
28 câu hỏi 60 phút
Một UAV (thiết bị bay không người lái) do Tập đoàn Viettel nghiên cứu và sản xuất sử dụng pin sạc có điện áp 24 V và dung lượng 12 Ah. Trong một lần hoạt động, UAV sử dụng một motor điện để duy trì bay với công suất trung bình 240 W và hiệu suất 80%. Giả sử pin được sạc đầy và toàn bộ năng lượng chỉ dùng cho motor bay. Thời gian tối đa UAV này có thể bay liên tục đến khi hết pin xấp xỉ bằng

0,96 giờ
1,2 giờ
1,5 giờ
3,6 giờ
Năng lượng của pin:
\(W=U.q=24.12.3600=1036800\) J.
Năng lượng motor điện nhận được:
\(A=H.W=80%.1036800=829440\) J.
Thời gian tối đa UAV có thể bay liên tục đến khi hết pin:
\(t=\dfrac{A}{\mathcal{P}}=\dfrac{829440}{240}=3456~s=0,96\) giờ.
Danh sách câu hỏi:
Năng lượng của pin:
\(W=U.q=24.12.3600=1036800\) J.
Năng lượng motor điện nhận được:
\(A=H.W=80%.1036800=829440\) J.
Thời gian tối đa UAV có thể bay liên tục đến khi hết pin:
\(t=\dfrac{A}{\mathcal{P}}=\dfrac{829440}{240}=3456~s=0,96\) giờ.
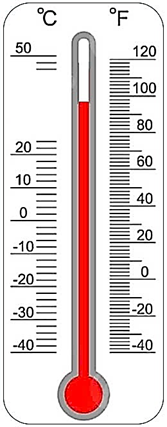
Do nhiệt độ đo được là hàm bậc nhất theo chiều dài cột thủy ngân nên ta có: \(t=a.\ell +b\).
Khi \(t=0~\), \(\ell =2\) cm, ta có: \(0=a.2+b\) \(2a+b=0\) (1)
Khi \(t=100~\), \(\ell =22\) cm, ta có: \(100=a.22+b\) \(22a+b=100\) (2)
Từ (1) và (2) ta có hệ phương trình sau:
\(\left\{\begin{array}{c}2 a+b=0 \\ 22 a+b=100\end{array} \Rightarrow\left\{\begin{array}{c}a=5 \\ b=-10\end{array}\right.\right.\)
Suy ra: \(t=5\ell -10\)
Nhiệt lượng cần cung cấp để 1 kg rượu tăng thêm 2 °C là
\(Q=m.c.T=1.2500.2=5000\) J.
Độ tăng nhiệt độ của miếng kim loại được xác định bằng biểu thức:
\(Q=m.c.T\) \(T=\dfrac{Q}{m.c}\)
Do các miếng kim loại có cùng khối lượng (m) và lần lượt được cung cấp một nhiệt lượng như nhau (Q) (bỏ qua sự trao đổi nhiệt ra môi trường) nên miếng kim loại nào có nhiệt dung riêng (c) nhỏ nhất sẽ tăng nhiệt độ nhiều nhất.
Vậy miếng chì tăng nhiệt độ nhiều nhất.
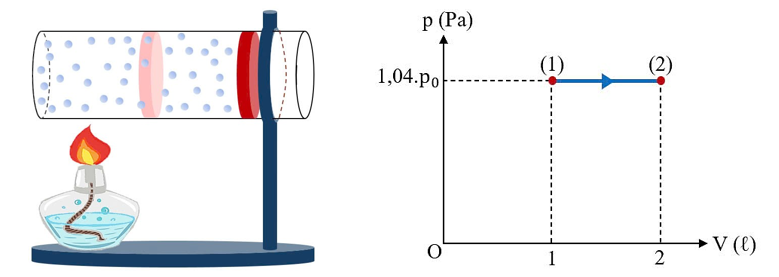
Theo nguyên lí I – nhiệt động lực học, ta có:
\(U=A+Q\) \(100=A+170\)
\(A=-70\) J.
Vậy khối khí đã thực hiện một công bằng 70 J.
Câu 16:
Cho các hạt nhân sau \({}_{92}^{238}\text{U}\), \({}_{92}^{235}\text{U}\), \({}_{11}^{23}\text{Na}\), \({}_{79}^{197}\text{Au}\). Biết rằng khối lượng của các hạt nhân \({}_{92}^{238}\text{U}\), \({}_{92}^{235}\text{U}\), \({}_{11}^{23}\text{Na}\), \({}_{79}^{197}\text{Au}\) và khối lượng của proton, neutron lần lượt là \({{\text{m}}_{\text{U}238}}\) = 238,050788 amu; \({{\text{m}}_{\text{U}235}}\) = 234,993422 amu, \({{\text{m}}_{\text{Na}23}}\) = 22,983730 amu, \({{\text{m}}_{\text{Au}197}}\) = 196,966552 amu, mp = 1,007276 amu và mn = 1,008665 amu. Lấy \(1\text{ }\!\!~\!\!\text{ u}{{\text{c}}^{2}}=931,5\text{ }\!\!~\!\!\text{ MeV}\). Thứ tự sắp xếp các hạt nhân nói trên theo mức độ bền vững tăng dần là
Câu 19:
Trong một phòng tắm, có một vòi hoa sen với nhiều lỗ phun nước nhỏ. Tổng diện tích các lỗ phun nước là S = 10 mm2 (thông số kỹ thuật do nhà sản xuất cung cấp). Trước khi ra khỏi vòi hoa sen, nước chảy qua một bộ phận đun nóng trực tiếp. Biết công suất tiêu thụ điện của bộ đun này là P = 2,8 kW; hiệu suất của bộ đun nóng là H = 95%; khối lượng riêng của nước là D = 1000 kg/m3; nhiệt dung riêng của nước là c = 4200 J/(kg.K); nhiệt độ của nước trước khi chảy vào bộ đun là \({{\text{t}}_{1}}\) = 20 °C và khi phun ra khỏi vòi hoa sen là \({{\text{t}}_{2}}\) = 36 °C. Bỏ qua sự tỏa nhiệt của nước ra môi trường. Xét trong khoảng thời gian 10 phút xả nước.

Nhiệt lượng do bộ đun nóng cung cấp cho nước là 168 kJ
Nhiệt lượng nước nhận được từ bộ phận đun nóng là 1596 kJ
Khối lượng nước được làm nóng là 23 kg
Tốc độ chảy trung bình của dòng nước vừa phun ra khỏi vòi hoa sen xấp xỉ bằng 4 m/s
Câu 20:
Một khối khí lí tưởng xác định thực hiện chu trình gồm các trạng thái (1) (2) (3) (4) (5). Đồ thị biểu diễn quá trình (1) (2) là một đường hypebol. Nhiệt độ của khối khí ở trạng thái (1) là 27 °C.
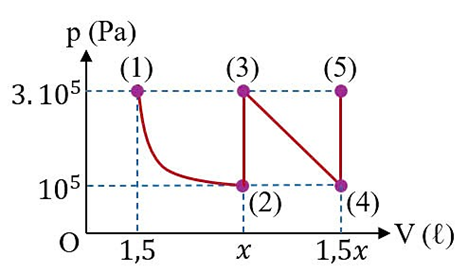
Số mol của khối khí lí tưởng xấp xỉ bằng 0,18 mol
Thể tích của khối khí ở trạng thái (2) bằng 4,5.10-3 m3
Khi khối khí biến đổi từ trạng thái (2) sang trạng thái (3), động năng tịnh tiến trung bình của mỗi phân tử khí tăng 3 lần
Nhiệt độ của khối khí ở trạng thái (5) là 300 K
Câu 21:
Một đoạn dây dẫn thẳng, nằm ngang được giữ cố định trong vùng từ trường đều giữa hai cực của một nam châm, sao cho đoạn dây dẫn vuông góc với các đường sức từ. Nam châm này được đặt trên một cái cân như hình bên. Chiều dài phần dây dẫn nằm trong từ trường đều là 4 cm. Khi không có dòng điện chạy trong đoạn dây dẫn, số chỉ của cân là 499,56 g. Khi có dòng điện cường độ 0,28 A chạy trong đoạn dây dẫn, số chỉ của cân là 500,12 g. Lấy \(\text{g}=9,8\) m/s2
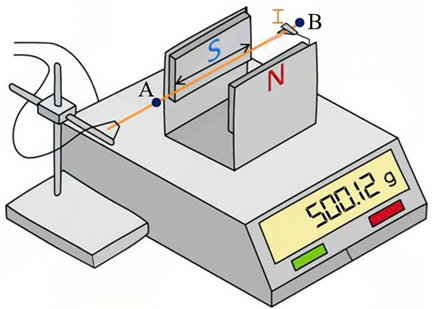
Số chỉ của cân tăng lên chứng tỏ trọng lượng của nam châm đã tăng
Dòng điện chạy trong đoạn dây dẫn đặt trong từ trường đều có chiều đi từ A đến B
Lực từ tác dụng lên đoạn dây dẫn đặt trong từ trường đều có độ lớn bằng 5,488 N
Độ lớn cảm ứng từ giữa hai cực của nam châm là 0,49 T
Câu 22:
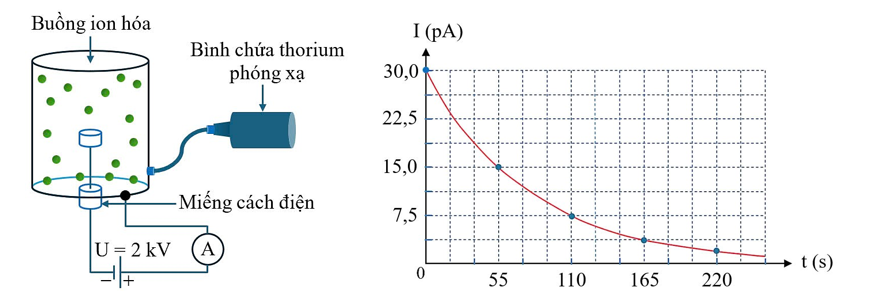
Khảo sát một bình ion hóa có cấu tạo là bình khí đơn nguyên tử và hai điện cực kim loại được đặt hiệu điện thế 2 kV. Khi khối khí này bị ion hóa nhờ tác dụng của tia phóng xạ thì sẽ có dòng điện chạy qua khối khí. Để đo dòng điện rất nhỏ này người ta dùng một ampe kế rất nhạy và thu được đồ thị biểu diễn như hình vẽ bên dưới.
Biết rằng độ phóng xạ tại thời điểm ban đầu là \({{\text{H}}_{0}}\). Hạt nhân 228Th phân rã α với chu kì bán rã là 1,9 năm thành 224Ra. Hạt nhân 224Ra phân rã α với chu kì bán rã 3,6 ngày thành 220Rn. Để dòng điện đủ lớn như trong thí nghiệm cần tối thiểu 1 mℓ lượng khí 220Rn ở điều kiện tiêu chuẩn (\(\text{p}=101325\text{ }\!\!~\!\!\text{ Pa}\); \(\text{t}=0\text{ }\!\!~\!\!\text{ }\)). Lấy 1 năm = 365 ngày, khối lượng của nguyên tử bằng số khối tính theo đơn vị amu.
Đồ thị biểu diễn sự biến thiên độ phóng xạ của mẫu 220Rn trong bình theo thời gian như hình vẽ sau:
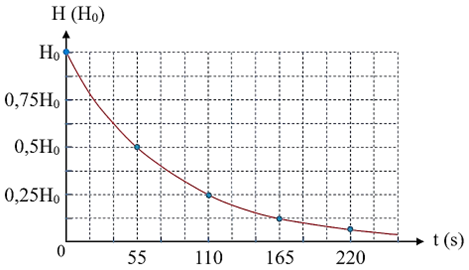
Chu kì bán rã của chất phóng xạ 220Rn là 55 giây
Số hạt nhân 220Rn có trong 1 mℓ khí 220Rn ở điều kiện tiêu chuẩn xấp xỉ bằng \(2,{{6887.10}^{19}}\) hạt
Khối lượng tối thiểu của chất phóng xạ 228Th để duy trì độ phóng xạ không đổi của 220Rn trước khi làm thí nghiệm xấp xỉ bằng 11094 g