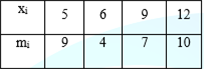
Cho \(X \sim B\left( {5;0.25} \right)\). Giá trị P(X > 3) bằng:
Đáp án đúng: D
Ta có \(X \sim B\left( {5;0.25} \right)\), tức là X tuân theo phân phối nhị thức với n = 5 và p = 0.25.
Ta cần tính P(X > 3) = P(X = 4) + P(X = 5).
Công thức tính xác suất trong phân phối nhị thức là: \(P(X = k) = C_n^k * p^k * (1-p)^(n-k)\)
Áp dụng vào bài toán:
\(P(X = 4) = C_5^4 * (0.25)^4 * (0.75)^1 = 5 * (0.25)^4 * 0.75 = 5 * 0.00390625 * 0.75 = 0.0146484375\)
\(P(X = 5) = C_5^5 * (0.25)^5 * (0.75)^0 = 1 * (0.25)^5 * 1 = 0.0009765625\)
Vậy, P(X > 3) = P(X = 4) + P(X = 5) = 0.0146484375 + 0.0009765625 = 0.015625
Chia sẻ hơn 467 câu trắc nghiệm Xác suất thống kê có đáp án dành cho các bạn sinh viên Đại học - Cao đăng ôn thi để đạt kết quả cao trong kì thi sắp diễn ra.
Câu hỏi liên quan
Để giải bài toán này, ta sẽ sử dụng phương pháp phần bù. Tính tổng số cách chọn 5 học sinh từ 9 học sinh, sau đó trừ đi các trường hợp không thỏa mãn điều kiện (tức là có lớp không có học sinh nào được chọn).
Tổng số cách chọn 5 học sinh từ 9 học sinh là: C(9, 5) = 9! / (5! * 4!) = (9 * 8 * 7 * 6) / (4 * 3 * 2 * 1) = 126.
Các trường hợp không thỏa mãn:
1. Chỉ có học sinh từ 12A và 12B được chọn: C(7, 5) = 7! / (5! * 2!) = (7 * 6) / (2 * 1) = 21.
2. Chỉ có học sinh từ 12A và 12C được chọn: C(6, 5) = 6! / (5! * 1!) = 6.
3. Chỉ có học sinh từ 12B và 12C được chọn: C(5, 5) = 1.
4. Chỉ có học sinh từ 12A được chọn: Không thể, vì cần chọn 5 học sinh mà lớp 12A chỉ có 4.
5. Chỉ có học sinh từ 12B được chọn: Không thể, vì cần chọn 5 học sinh mà lớp 12B chỉ có 3.
6. Chỉ có học sinh từ 12C được chọn: Không thể, vì cần chọn 5 học sinh mà lớp 12C chỉ có 2.
Nhưng ta cần phải cộng lại các trường hợp mà ta đã trừ đi quá nhiều lần:
Không có trường hợp nào đồng thời chỉ chọn học sinh từ một lớp khác.
Số cách chọn thỏa mãn là: 126 - (21 + 6 + 1) = 126 - 28 = 98.
Vậy có 98 cách chọn sao cho lớp nào cũng có học sinh được chọn.
Để chọn 4 viên bi sao cho số bi xanh bằng số bi đỏ, ta có các trường hợp sau:
- 2 bi xanh, 2 bi đỏ, 0 bi vàng: Số cách chọn là C(8,2) * C(5,2) * C(3,0) = (8!/(2!6!)) * (5!/(2!3!)) * (3!/(0!3!)) = 28 * 10 * 1 = 280
- 1 bi xanh, 1 bi đỏ, 2 bi vàng: Số cách chọn là C(8,1) * C(5,1) * C(3,2) = (8!/(1!7!)) * (5!/(1!4!)) * (3!/(2!1!)) = 8 * 5 * 3 = 120
- 0 bi xanh, 0 bi đỏ, 4 bi vàng: Trường hợp này không thể xảy ra vì chỉ có 3 bi vàng.
Vậy tổng số cách chọn là 280 + 120 = 400.
* Trường hợp 1: Số bi đỏ là 4, số bi vàng là 0. Số bi xanh có thể là 0.
Số cách chọn là C(5,4) * C(3,0) * C(4,0) = 5 * 1 * 1 = 5
* Trường hợp 2: Số bi đỏ là 3, số bi vàng là 0 hoặc 1. Số bi xanh có thể là 1 hoặc 0.
* Số bi đỏ là 3, số bi vàng là 0, số bi xanh là 1: C(5,3) * C(3,0) * C(4,1) = 10 * 1 * 4 = 40
* Số bi đỏ là 3, số bi vàng là 1, số bi xanh là 0: C(5,3) * C(3,1) * C(4,0) = 10 * 3 * 1 = 30
* Trường hợp 3: Số bi đỏ là 2, số bi vàng là 0 hoặc 1. Số bi xanh có thể là 2 hoặc 1.
* Số bi đỏ là 2, số bi vàng là 0, số bi xanh là 2: C(5,2) * C(3,0) * C(4,2) = 10 * 1 * 6 = 60
* Số bi đỏ là 2, số bi vàng là 1, số bi xanh là 1: C(5,2) * C(3,1) * C(4,1) = 10 * 3 * 4 = 120
* Trường hợp 4: Số bi đỏ là 1, số bi vàng là 0. Số bi xanh là 3.
* Số bi đỏ là 1, số bi vàng là 0, số bi xanh là 3: C(5,1) * C(3,0) * C(4,3) = 5 * 1 * 4 = 20
Tổng số cách là 5 + 40 + 30 + 60 + 120 + 20 = 275.
Vậy, có 275 cách lấy ra 4 viên bi sao cho số bi đỏ lớn hơn số bi vàng.
\(\left( {\overline x - \frac{{{u_{\alpha /2}}\sigma }}{{\sqrt n }};\overline x + \frac{{{u_{\alpha /2}}\sigma }}{{\sqrt n }}} \right)\)
Trong đó:
* \(\overline x\) là trung bình mẫu.
* \(\sigma\) là độ lệch chuẩn của tổng thể (đã biết).
* \(n\) là kích thước mẫu.
* \({u_{\alpha /2}}\) là giá trị tới hạn từ phân phối chuẩn tắc tương ứng với mức ý nghĩa \(\alpha/2\).
Do đó, đáp án đúng là phương án 1. Các phương án khác không đúng vì chúng đưa ra các khoảng tin cậy không đối xứng hoặc không phù hợp với công thức ước lượng khoảng tin cậy cho kỳ vọng của biến ngẫu nhiên tuân theo phân phối chuẩn với độ lệch chuẩn đã biết.
- Phương án 1: \(U = \frac{{\left( {\overline X - {\mu _0}} \right)}}{\sigma }\sqrt n\) là thống kê kiểm định cho giá trị trung bình của một tổng thể khi độ lệch chuẩn của tổng thể đã biết.
- Phương án 2: \(T = \frac{{\overline X - {\mu _0}}}{{S'}}\sqrt n\) là thống kê kiểm định cho giá trị trung bình của một tổng thể khi độ lệch chuẩn của tổng thể chưa biết (ước lượng bằng độ lệch chuẩn mẫu).
- Phương án 3: \({\chi ^2} = \frac{{n{S^{*2}}}}{{\sigma _0^2}}\) là thống kê kiểm định cho phương sai của một tổng thể.
- Phương án 4: \(U = \frac{{\left( {f - {p_0}} \right)}}{{\sqrt {{p_0}\left( {1 - {p_0}} \right)} }}\sqrt n\) là thống kê kiểm định cho xác suất (tỷ lệ) p của một tổng thể, với f là tỷ lệ mẫu.
Vì vậy, phương án đúng là phương án 4.
