Xét hàm số \(f\left( x \right)=\left| \frac{mx-2\sqrt{x+4}}{2x+4} \right|\) với \(m\) là tham số thực. Có tất cả bao nhiêu số nguyên \(m\) thỏa mãn điều kiện \(0 < \underset{\left[ -1;1 \right]}{\mathop{\min }}\,f\left( x \right) < 1\)?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(g\left( x \right)=\frac{mx-2\sqrt{x+4}}{2x+4}\), \(x\in \left[ -1;1 \right]\).
Nếu \(g\left( x \right)=0\) có nghiệm thuộc đoạn \(\left[ -1;1 \right]\) thì \(\underset{\left[ -1;1 \right]}{\mathop{\min }}\,f\left( x \right)=0\), không thỏa mãn điều kiện \(0 < \underset{\left[ -1;1 \right]}{\mathop{\min }}\,f\left( x \right) < 1\).
Do đó để có \(0 < \underset{\left[ -1;1 \right]}{\mathop{\min }}\,f\left( x \right) <1\) thì điều kiện cần là phương trình \(g\left( x \right)=0\) không có nghiệm thuộc đoạn \(\left[ -1;1 \right]\).
Trên đoạn \(\left[ -1;1 \right]\): \(g\left( x \right)=0\Leftrightarrow \frac{mx-2\sqrt{x+4}}{2x+4}=0\)\( \Leftrightarrow mx-2\sqrt{x+4}=0\)\( \Leftrightarrow m=\frac{2\sqrt{x+4}}{x}\).
Đặt \(h\left( x \right)=\frac{2\sqrt{x+4}}{x}\) với \(x\in \left[ -1;1 \right]\backslash \left\{ 0 \right\}\).
Ta có \({h}'\left( x \right)=\frac{-x-8}{{{x}^{2}}\sqrt{x+4}}<0\), \(\forall x\in \left[ -1;1 \right]\backslash \left\{ 0 \right\}\).
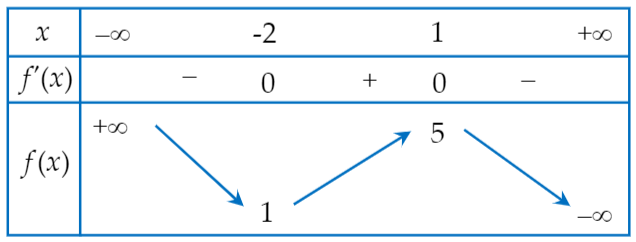
Bảng biến thiên của \(h\left( x \right)\) với \(x\in \left[ -1;1 \right]\backslash \left\{ 0 \right\}\).
.PNG)
Do đó để không có nghiệm thuộc đoạn \(\left[ -1;1 \right]\) thì ta phải có \(m\in \left( -2\sqrt{3};2\sqrt{5} \right)\).
Ta có \({g}'\left( 0 \right)=\frac{2m+3}{8}=0\)\( \Leftrightarrow m=-\frac{3}{2}\).
Vậy nếu \(m\) nguyên thì \(x=0\) không phải là điểm cực trị của \(g\left( x \right)\), do đó \(f\left( x \right)\) không thể đạt giá trị nhỏ nhất tại \(x=0\).’
Mà \(f\left( 0 \right)=1\).
Do đó với \(m\) nguyên, \(m\in \left( -2\sqrt{3};2\sqrt{5} \right)\) thì \(0 < \underset{\left[ -1;1 \right]}{\mathop{\min }}\,f\left( x \right) < 1\).
Vậy \(m\in \left\{ -3;-1;...;3;4 \right\}\).
Chọn B
Đề thi thử Tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Trần Khai Nguyên
Câu hỏi liên quan
-
Trong không gian \(Oxyz\) cho mặt cầu \((S):(x+2)^{2}+y^{2}+(z+5)^{2}=24\) cắt mp \((\alpha): x+y+4=0\) theo giao tuyến là đường tròn \((C)\). Điểm \(M\) thuộc \((C)\) sao cho khoàng cách từ \(M\) đến \(A(4 ;-12 ; 1)\) nhỏ nhất có tung độ bằng?
-
Trong không gian \(Oxyz,\) cho mp \(\left( P \right):\,2x+y-z+3=0\). Điểm nào sau đây không thuộc mặt phẳng \(\left( P \right)\)?
-
Tập nghiệm của bất phương trình sau \(\log _{2}^{2}\left( 2x \right)+1\le {{\log }_{2}}\left( {{x}^{5}} \right)\) là?
-
Với \(a,b\) là các số thực dương tùy ý, ta có \(\log \left( {{a}^{5}}{{b}^{10}} \right)\) bằng?
-
Cho các số phức sau \(z=2+i\) và \(\omega =3-2i\). Phần ảo của số phức \(z+2\omega \) bằng?
-
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(\log _{3}^{2}x-m{{\log }_{9}}{{x}^{2}}+2-m=0\) có nghiệm \(x\in \left[ 1;9 \right]\)?
-
Cho HS \(f\left( x \right)\) thỏa mãn \(f\left( 0 \right)=\frac{2}{3}\) và \(\left( \sqrt{x}+\sqrt{x+1} \right).{f}'\left( x \right)=1,\forall x\ge -1\). Biết \(\int\limits_{0}^{1}{f\left( x \right)dx}=\frac{a\sqrt{2}+b}{15}\) với \(a,b\in \mathbb{Z}\). Tính \(T=a+b\)?
-
Cho khối lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có đáy \(ABC\) là tam giác vuông cân tại \(C\), \(AB=2a\) và góc tạo bởi 2 mặt phẳng \(\left( AB{C}' \right)\) và \(\left( ABC \right)\) bằng \(60{}^\circ \). Gọi \(M,N\) lần lượt là trung điểm của \({A}'{C}'\) và \(BC\). Mặt phẳng \(\left( AMN \right)\) chia khối lăng trụ thành hai phần. Thể tích của phần nhỏ bằng?
-
Cho số phức \(z=2i+1\). Điểm nào dưới đây là điểm biểu diễn của số phức \(z\) trên mặt phẳng tọa độ?
-
TXĐ của hàm số \(y={{\left( 2-x \right)}^{\frac{1}{2}}}\) là?
-
Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mp \(\left( ABC \right)\), \(SA=1\) và đáy \(ABC\) là tam giác đều với độ dài cạnh bằng 2. Tính góc giữa mặt phẳng \(\left( SBC \right)\) và mặt phẳng \(\left( ABC \right)\)?
-
Cho HS \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\), có đồ thị \({f}'\left( x \right)\) như hình:
.PNG)
Số điểm cực tiểu của hàm số \(g\left( x \right)=f\left( -{{x}^{2}}+x \right)\) là?
-
Cho \({{z}_{1}}\), \({{z}_{2}}\) là các nghiệm phức phân biệt của phương trình sau \({{z}^{2}}-4z+13=0\). Tính \({{\left| {{z}_{1}}+i \right|}^{2}}+{{\left| {{z}_{2}}+i \right|}^{2}}\)?
-
TXĐ của hàm số \({y=\sqrt{\log _{\frac{1}{2}}\left(x^{2}+7 x\right)+3}}\) là?
-
Cho CSC \(\left( {{u}_{n}} \right)\) có số hạng đầu \({{u}_{1}}=2\) và số hạng thứ tư \({{u}_{4}}=17\). Công sai của cấp số cộng đã cho bằng?
-
Cho hình trụ có bán kính đáy bằng \(a\sqrt{3}\). Cắt hình trụ bởi 1 mặt phẳng song song với trục, cách trục 1 khoảng bằng a ta được thiết diện là một hình vuông. Thể tích khối trụ đó bằng?
-
Trong không gian \(Oxyz,\) hình chiếu vuông góc của điểm \(M\left( 3;\,1;\,2 \right)\) lên trục \(Oy\) là điểm nào?
-
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị là đường cong như hình vẽ:
Số nghiệm của phương trình \(2f\left( x \right)+1=0\) là?
-
Cho hàm số sau
\(f\left( x \right)=\left\{ \begin{align} & 3{{x}^{2}}\ln \left( x+1 \right)\text{ khi }x\ge 0 \\ & 2x\sqrt{{{x}^{2}}+3}+1\text{ khi }x<0 \\ \end{align} \right.\).
Biết \(\int\limits_{\frac{1}{e}}^{e}{\frac{f\left( \ln x \right)}{x}dx}=a\sqrt{3}+b\ln 2+c\) với \(a,b,c\in \mathbb{Q}\). Giá trị của \(a+b+6c\) bằng?
-
Đường TCĐ của đồ thị hàm số \(y=\frac{x}{x-1}\) là?
