Trong không gian OxyzOxyz, cho mặt cầu (S):(x+1)2+(y−1)2+z2=4(S):(x+1)2+(y−1)2+z2=4 và hai điểm A(1;2;4)A(1;2;4), B(0;0;1)B(0;0;1). Mặt phẳng (P):ax+by+cz+3=0(P):ax+by+cz+3=0 (a,b,c∈R) đi qua A,B và cắt (S) theo giao tuyến là 1 đường tròn có bán kính nhỏ nhất. Giá trị của a+b+c bằng?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai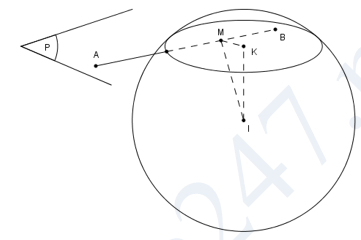
Mặt cầu (S) có tâm I(−1;1;0) và bán kính R=2.
Ta có IA=√21, IB=√3 nên A nằm ngoài (S), B nằm trong (S). Do đó mặt phẳng (P) luôn cắt (S) theo một đường tròn (C) tâm K bán kính r.
Gọi M là hình chiếu vuông góc của I trên đường thẳng AB.
Ta có IK=d(I,(P)) và r2=R2−IK2.
Ta có IK⊥(P) ⇒IK≤IM ⇒r2≥R2−IM2.
Đẳng thức xảy ra khi IM⊥(P). Khi đó
→n(P)=(→AB∧→IA)∧→AB=(12;−18;8).
Vì R;IM không đổi nên r có giá trị nhỏ nhất bằng √R2−IM2.
Khi đó phương trình mặt phẳng (P) là
12(x−0)−18(y−0)+8(z−1)=0⇔ 12x−18y+8z−8=0⇔ −92x+274y−3z+3=0.
Vậy a+b+c=−92+274−3=−34.
Chọn B
Đề thi thử tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Minh Đức















