Cho phương trình \({7^x} + m = {\log _7}\left( {x - m} \right)\) với m là tham số. Có bao nhiêu giá trị nguyên của \(m \in \left( { - 25;25} \right)\) để phương trình đã cho có nghiệm ?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(\begin{array}{l}\,\,\,\,\,{7^x} + m = {\log _7}\left( {x - m} \right)\\ \Leftrightarrow {7^x} + x = x - m + {\log _7}\left( {x - m} \right)\\ \Leftrightarrow {7^x} + x = {7^{{{\log }_7}\left( {x - m} \right)}} + {\log _7}\left( {x - m} \right)\,\,\,\left( * \right)\end{array}\)
Xét hàm số \(f\left( x \right) = {7^x} + x \Rightarrow f'\left( x \right) = {7^x}\ln 7 + 1 > 0 \Rightarrow \) Hàm số đồng biến trên R
\(\left( * \right) \Rightarrow x = {\log _7}\left( {x - m} \right) \Leftrightarrow {7^x} = x - m \Leftrightarrow m = x - {7^x}\)
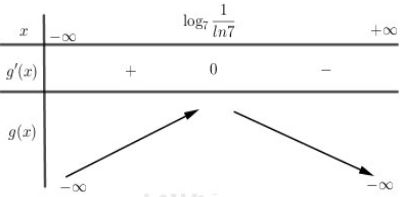
Xét hàm số \(g\left( x \right) = x - {7^x}\) có \(g'\left( x \right) = 1 - {7^x}\ln 7 = 0 \Leftrightarrow {7^x} = \dfrac{1}{{\ln 7}} \Leftrightarrow x = {\log _7}\dfrac{1}{{\ln 7}}\)
Lập BBT:
\( \Rightarrow \) Để phương trình có nghiệm thì \(m \in \left( { - \infty ;g\left( {{{\log }_7}\dfrac{1}{{\ln 7}}} \right)} \right)\)
Kết hợp điều kiện đề bài \( \Rightarrow m \in \left( { - 25;g\left( {{{\log }_7}\dfrac{1}{{\ln 7}}} \right)} \right);\,\,g\left( {{{\log }_7}\dfrac{1}{{\ln 7}}} \right) \approx - 0,85\)
Mà \(m \in Z \Rightarrow \) có 24 giá trị thỏa mãn.
Chọn C.
Đề thi thử THPT QG năm 2022 môn Toán
Trường THPT Lê Văn Đẩu
Câu hỏi liên quan
-
Cho a > 0, b > 0 thoả mãn \({\log _{4a + 5b + 1}}\left( {16{a^2} + {b^2} + 1} \right) + {\log _{8ab + 1}}\left( {4a + 5b + 1} \right) = 2\). Giá trị của a + 2b bằng
-
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn [-2 ; 2] và có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình \(3f\left( x \right) - 4 = 0\) trên đoạn \(\left[ { - 2;2} \right]\) là
.JPG)
-
Cho hai hàm số \(y = f\left( x \right),y = g\left( x \right)\). Hai hàm số \(y = f'\left( x \right),y = g'\left( x \right)\)có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số \(y = g'\left( x \right)\). Hàm số \(h\left( x \right) = f\left( {x + 3} \right) - g\left( {2x - \dfrac{7}{2}} \right)\) đồng biến trên khoảng nào dưới đây ?
-
Thể tích của khối trụ tròn xoay có bán kính đáy r và chiều cao h bằng
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh \(\sqrt 3 a\) , SA vuông góc với mặt phẳng đáy và \(SA = a\). Khoảng cách từ A đến mặt phẳng (SBC) bằng
-
Cho hàm số \(y = a{x^4} + b{x^2} + c\left( {a,b,c \in R} \right)\) có đồ thị như hình vẽ bên.
.JPG)
Số điểm cực trị của hàm số đã cho là
-
Cho hình phẳng (H) giới hạn bởi các đường \(y = {x^2} + 3,y = 0,x = 0,x = 2\). Gọi V là thể tích của khối tròn xoay được tạo thành khi quay (H) xung quang trục Ox. Mệnh đề nào dưới đây đúng?
-
Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{\left( {x + 3} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 1} \right)^2} = 2\) . Tâm của (S) có tọa độ là
-
Với α là số thực dương tùy ý, \(\ln \left( {7a} \right) - \ln \left( {3a} \right)\) bằng
-
Cho hình lập phương ABCD.A’B’C’D’ có tâm O. Gọi I là tâm của hình vuông A’B’C’D’ và M là điểm thuộc đoạn thẳng OI sao cho MO = 2MI (tham khảo hình vẽ). Khi đó sin của góc tạo bởi hai mặt phẳng (MC’D’) và (MAB) bằng
.JPG)
-
Cho hàm số \(y = \dfrac{1}{3}{x^4} - \dfrac{{14}}{3}{x^2}\) có đồ thị (C). Có bao nhiêu điềm A thuộc (C) sao cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt \(M\left( {{x_1};{y_1}} \right);N\left( {{x_2};{y_2}} \right)\) (M, N khác A) thoả mãn \({y_1} - {y_2} = 8\left( {{x_1} - {x_2}} \right)\) ?
-
Tìm hai số thực x và y thỏa mãn \(\left( {3x + yi} \right) + \left( {4 - 2i} \right) = 5x + 2i\) với i là đơn vị ảo.
-
Số phức 5 + 6i có phần thực bằng
-
Cho \(\int\limits_1^e {\left( {1 + x\ln x} \right)dx = a{e^2} + be + c} \) với a, b, c là các số hữu tỉ. Mệnh đề nào dưới đây đúng?
-
Từ các chữ số \(1,2,3,4,5,6,7\) lập được bao nhiêu số tự nhiên gồm hai chữ số khác nhau?
-
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
.JPG)
-
Cho khối lăng trụ \(ABC.A'B'C'\), khoảng cách từ C đến đường thẳng BB’ bằng 2, khoảng cách từ A đến các đường thẳng BB’ và CC’ lần lượt bằng 1 và \(\sqrt 3 \), hình chiếu vuông góc của A lên mặt phẳng (A’B’C’) là trung điểm M của B’C’ và A’M = 2. Thể tích của khối lăng trụ đã cho bằng
-
Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = {x^8} + \left( {m - 4} \right){x^5} - \left( {{m^2} - 16} \right){x^4} + 1\) đạt cực tiểu khi \(x = 0\)?
-
Cho hàm số \(y = \frac{{x - 2}}{{x + 2}}\) có đồ thị (C). Gọi I là giao điểm của hai tiệm cận của (C). Xét tam giác đều ABI có hai đỉnh A, B thuộc (C), đoạn thẳng AB có độ dài bằng
-
Trong không gian Oxyz, mặt phẳng \(\left( P \right):2x + 3y + z-1 = 0\) có một vectơ pháp tuyến là
