Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O; cạnh a. Goi M, N lần lượt là trung điểm của SA và BC. Góc giữa đường thằng M N và mặt phẳng (A B C D) bằng \(60^{\circ} .\) Tính cos của góc giũa đương thằng MN và măt phẳng (SBD) ?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai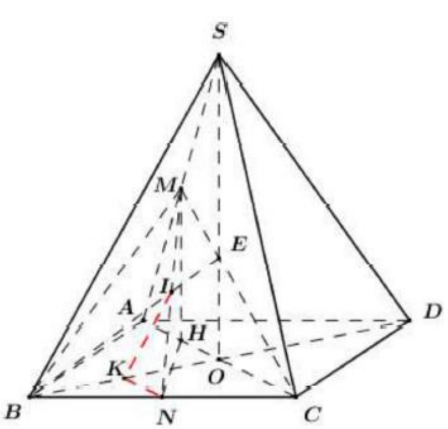
Goi H là trung điểm của OA ta có M H//S O \(\Rightarrow M H \perp(A B C D)\)
\(\Rightarrow H N\) là hinh chiếu của MN lên (A B C D) \\(\Rightarrow \widehat{(M N ;(A B C D))}=\widehat{M N ; H N}=\widehat{ M N H}=60^{\circ}\)
Xét tam giác CHN có: \(C N=\frac{1}{2} B C=\frac{a}{2}, C H=\frac{3}{4} A C=\frac{3 a \sqrt{2}}{4}, \widehat{{ H C N}}=45^{\circ}\)
\(\Rightarrow H N^{2}=C H^{2}+C N^{2}-2 C H \cdot C N \cdot \cos 45^{0}\)
\(H N^{2}=\frac{9 a^{2}}{8}+\frac{a^{2}}{4}-2 \cdot \frac{3 a \sqrt{2}}{4} \cdot \frac{a}{2} \cdot \frac{\sqrt{2}}{2}\\
H N^{2}=\frac{5 a^{2}}{8} \Rightarrow H N=\frac{a \sqrt{10}}{4}\)
Xét tam giác vuông MNH có: \(M N=\frac{N H}{\cos 60^{\circ}}=\frac{a \sqrt{10}}{2}\)
Trong (SAC) gọi \(E=C M \cap S O \Rightarrow(M B C) \cap(S B D)=B E\)
Trong (M B C) goi \(I=M N \cap B E \Rightarrow I=M N \cap(S B D)\)
Gọi K là trung điểm của O B \(\Rightarrow N K // O C\)
Ta có: \(\left\{\begin{array}{l}O C \perp B D \\ O C \perp S O\end{array} \Rightarrow O C \perp(S B D) \Rightarrow N K \perp(S B D)\right.\)
\(\Rightarrow I K\) là hinh chiếu của IN lên (S B D) \(\Rightarrow \widehat{(M N ;(S B D))}=\widehat{(I N ;(S B D))}=\widehat{(I N ; I K)}=\widehat{ N I K}\)
Ta có \(N K=\frac{1}{2} O C=\frac{a \sqrt{2}}{4}\)
Áp dụng định lí Menelaus trong tam giác MAC ta có:
\(\frac{E M}{E C} \cdot \frac{O C}{O A} \cdot \frac{S A}{S M}=1 \Leftrightarrow \frac{E M}{E C} \cdot 1.2=1 \Leftrightarrow \frac{E M}{E C}=\frac{1}{2}\)
Áp dụng định lý Menelaus trong tam giác MNC ta có:
\(\frac{I M}{I N} \cdot \frac{B N}{B C} \cdot \frac{E C}{E M}=1 \Leftrightarrow \frac{I M}{I N} \cdot \frac{1}{2} \cdot 2=1 \Leftrightarrow I M=I N\)
\(\Rightarrow I N=\frac{1}{2} M N=\frac{a \sqrt{10}}{4}\)
Xét tam giác vuông INK có : \(\sin \widehat{ N I K}=\frac{N K}{I N}=\frac{a \sqrt{2}}{4}: \frac{a \sqrt{10}}{4}=\frac{1}{\sqrt{5}}\)
\(\cos\widehat{ N I K}=\sqrt{1-\sin ^{2}\widehat{ N I K}}=\sqrt{1-\frac{1}{5}}=\frac{2 \sqrt{5}}{5}\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT chuyên Thái Bình