Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Cạnh AC = a, \(BC = a\sqrt 5 \). Mặt phẳng (SAB) vuông góc mặt phẳng đáy và tam giác SAB đều. Gọi K điểm thuộc cạnh SC sao cho SC = 3SK. Tính khoảng cách \(d\) giữa hai đường thẳng AC và BK theo a.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi H là trung điểm của AB \( \Rightarrow SH \bot AB\) (do tam giác SAB đều)
Do \((SAB) \bot (ABC) \Rightarrow SH \bot (ABC)\)
Do tam giác ABC vuông tại A nên AB=2a\( \Rightarrow SH = a\sqrt 3 .\)
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.2a.a = {a^2}\)
Kẻ KM song song với AC cắt SA tại M. Khi đó AC//KM suy ra AC//(BKM)
Do đó d(AC,BK)=d(AC,(BKM))
Ta có \(AC \bot AB;AC \bot SH\) nên \(AC \bot (SAB)\)
Kẻ \(AI \bot BM,\) do KM//AC nên \(AI \bot KM\) suy ra \(AI \bot \left( {BKM} \right)\)
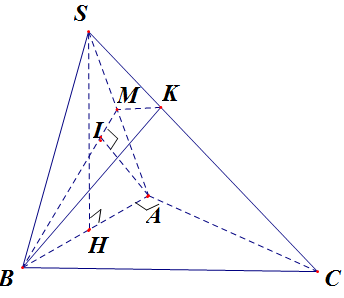
Suy ra d(AC,BK)=d(AC,(BKM))=d(A,(BKM))=AI
Ta có: \(\frac{{MA}}{{SA}} = \frac{{KC}}{{SC}} = \frac{2}{3} \Rightarrow {S_{AMB}} = \frac{2}{3}{S_{SAB}} = \frac{2}{3}{(2a)^2}\frac{{\sqrt 3 }}{4} = \frac{2}{3}{a^2}\sqrt 3 .\)
Ta lại có \(BM = \sqrt {A{B^2} + A{M^2} - AB.AM.\cos {{60}^0}} = \frac{{2a\sqrt 7 }}{3}\)
Do đó \(AI = \frac{{2{S_{ABM}}}}{{BM}} = \frac{{2\sqrt {21} a}}{7}.\) Vậy \(d(AC,BK) = \frac{{2\sqrt {21} a}}{7}.\)
Đáp án C
Đề thi thử THPT QG năm 2023 môn Toán
Trường THPT Nguyễn Thị Diệu
