Khối chóp S.ABCD có đáy là hình thoi cạnh a, \(SA=SB=SC=a\), cạnh SD thay đổi. Thể tích khối chóp S.ABCD lớn nhất khi độ dài cạnh SD là:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiKhối chóp S.ABCD có đáy là hình thoi cạnh a, \(SA=SB=SC=a\)\(\Rightarrow \) Khối chóp S.ABC có: \(SA=SB=SC=BA=BC=a\) và có thể tích bằng \(\frac{1}{2}\) thể tích khối chóp S.ABCD. Như vậy, để thể tích khối chóp S.ABCD lớn nhất thì thể tích khối chóp S.ABC lớn nhất khi SD thay đổi.
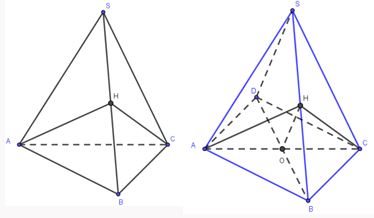
Gọi H là trung điểm của SB.
\(\Delta SAB,\,\,\Delta SBC\) là 2 tam giác đều, cạnh a \(\Rightarrow AH=CH=\frac{a\sqrt{3}}{2}\)
Và \(AH\bot SB,\,\,CH\bot SB\Rightarrow SB\bot (AHC)\Rightarrow {{V}_{S.ABC}}=\frac{1}{3}.SB.{{S}_{AHC}}=\frac{1}{3}a.{{S}_{AHC}}\)
Mặt khác \({{S}_{AHC}}=\frac{1}{2}.AH.CH.\sin \widehat{AHC}=\frac{1}{2}.{{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}\sin \widehat{AHC}\)
\(\Rightarrow {{V}_{S.ABC}}\) lớn nhất khi và chỉ khi \(\widehat{AHC}={{90}^{0}}\Leftrightarrow AH\bot HC\Rightarrow \Delta AHC\) vuông cân tại H \(\Rightarrow HO=\frac{AH}{\sqrt{2}}=\frac{\frac{a\sqrt{3}}{2}}{\sqrt{2}}=\frac{a\sqrt{3}}{2\sqrt{2}}\)
OH là đường trung bình của \(\Delta SBD\) \(\Rightarrow SD=2.OH=2.\frac{a\sqrt{3}}{2\sqrt{2}}=\frac{a\sqrt{3}}{\sqrt{2}}=\frac{a\sqrt{6}}{2}\)
Vậy, để thể tích khối chóp S.ABCD lớn nhất khi độ dài cạnh SD là: \(\frac{a\sqrt{6}}{2}\).
Chọn: C
Đề thi thử THPT QG năm 2023 môn Toán
Trường THPT Nguyễn Thị Diệu



.png)












