Cho hàm số \(f(x)=\left| {{x}^{3}}-3{{x}^{2}}+m \right|\) với \(m\in \left[ -5;7 \right]\) là tham số. Có bao nhiêu giá trị nguyên của m để hàm số \(f\left( x \right)\) có đúng 3 điểm cực trị?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai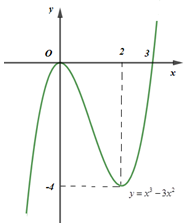
Quan sát đồ thị hàm số \(y={{x}^{3}}-3{{x}^{2}}\), ta thấy:
+) Nếu \(m=0\) thì hàm số \(f\left( x \right)=\left| {{x}^{3}}-3{{x}^{2}}+m \right|=\left| {{x}^{3}}-3{{x}^{2}} \right|\) đạt cực trị tại 3 điểm : \(x=0,\,\,x=2,\,\,x=3\).
+) Nếu \(m=4\) thì hàm số \(f\left( x \right)=\left| {{x}^{3}}-3{{x}^{2}}+m \right|=\left| {{x}^{3}}-3{{x}^{2}}+4 \right|\) đạt cực trị tại 3 điểm : \(x=0,\,\,x=2,\,\,x=-1\).
+) Nếu \(m\ne 0,\,\,m\ne 4\) thì số cực trị của hàm số \(f\left( x \right)=\left| {{x}^{3}}-3{{x}^{2}}+m \right|\) bằng tổng của số giao điểm của \(y={{x}^{3}}-3{{x}^{2}}\) với Ox và 2 ( là 2 cực trị của hàm số \(y={{x}^{3}}-3{{x}^{2}}\))
Do đó, để hàm số \(f\left( x \right)=\left| {{x}^{3}}-3{{x}^{2}}+m \right|\) có đúng 3 điểm cực trị thì đồ thị hàm số \(y={{x}^{3}}-3{{x}^{2}}\) với Ox \( \Rightarrow \left[ \begin{array}{l}m > 0\\m < 4\end{array} \right.\)
Vậy, để hàm số \(f\left( x \right)=\left| {{x}^{3}}-3{{x}^{2}}+m \right|\) có đúng 3 điểm cực trị thì \(\left[ \begin{align} & m\ge 0 \\ & m\le -4 \\\end{align} \right.\)
Mà \(m\in \left[ -5;7 \right]\Rightarrow m\in \left\{ -5;-4;\,0;1;2;3;4;5;6;7 \right\}\). Có 10 giá trị của m thỏa mãn.
Chọn: C
Đề thi thử THPT QG năm 2023 môn Toán
Trường THPT Nguyễn Thị Diệu
Câu hỏi liên quan
-
Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng \(R\sqrt{3}\). Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho khoảng cách giữa AB và truc của hình trụ bằng \(\frac{R\sqrt{3}}{2}\). Góc giữa AB và trục của hình trụ bằng:
-
Cho \(f(x)=a.\ln \left( x+\sqrt{{{x}^{2}}+1} \right)+b.{{x}^{2017}}+2018\) với \(a,b\in R\). Biết rằng \(f\left( \log \left( \log e \right) \right)=2019\). Tính giá trị của \(f\left( \log \left( \ln 10 \right) \right)\).
-
Đồ thị hàm số \(y={{x}^{4}}-{{x}^{3}}-3\) cắt trục tung tại mấy điểm
-
Rút gọn biểu thức \(A=\frac{\sqrt[3]{{{a}^{8}}}.{{a}^{\frac{7}{3}}}}{{{a}^{5}}.\sqrt[4]{{{a}^{-3}}}}\) với \(a>0\) ta được kết quả \(A={{a}^{\frac{m}{n}}}\), trong đó \(m,n\in {{N}^{*}}\) và \(\frac{m}{n}\) là phân số tối giản. Khẳng định nào sau đây đúng?
-
Cho hàm số \(y=f(x)\) có đạo hàm \(f'\left( x \right)=2018{{\left( x-1 \right)}^{2017}}{{\left( x-2 \right)}^{2018}}{{\left( x-3 \right)}^{2019}}\). Tìm số điểm cực trị của \(f(x)\).
-
Có 2 kiểu đồng hồ đeo tay (vuông, tròn) và 3 kiểu dây (kim loại, da, nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?
-
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau
.png)
Tìm tất cả các giá trị của m để phương trình \(f\left( x \right)=m\) có đúng 2 nghiệm.
-
Cho hàm số \(f(x)={{x}^{3}}+a{{x}^{2}}+bx-2\) thỏa mãn \(\left\{ \begin{array}{l}a + b > 1\\3 + 2a + b < 0\end{array} \right.\). Số điểm cực trị của hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) là:
-
Hàm số \(y=\sqrt{{{x}^{2}}-2x}\) nghịch biến trên khoảng nào?
-
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa A’C’ và D’C là:
-
Trong không gian với hệ tọa độ Oxyz, cho điểm \(M\left( 1;3;-2 \right)\). Gọi (P) là mặt phẳng đi qua điểm M và cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng (P) cắt trục Oy tại điểm B. Tọa độ điểm B là:
-
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với đáy. Gọi M là trung điểm AC. Khẳng định nào sau đây sai?
-
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số \(y=\frac{x-3}{{{x}^{2}}-2mx+1}\) có 2 đường tiệm cận đứng.
-
Trong không gian với hệ tọa độ Oxyz, phương trình nào sau đây là phương trình chính tắc của đường thẳng đi qua hai điểm \(A\left( 1;2;-3 \right),\,\,B\left( 7;0;-1 \right)\)?
-
Cho mặt cầu (S) tâm I bán kính R. Một mặt phẳng cắt mặt cầu (S) và cách tâm I một khoảng bằng \(\frac{R}{2}\). Bán kính của đường tròn do mặt phẳng cắt mặt cầu tạo nên là:
-
Cho \(0<a\ne 1,\,\,\,\,x>0,\,\,y>0\). Chọn mệnh đề đúng trong các mệnh đề sau
-
Giả sử \(F(x)\) là một nguyên hàm của hàm số \(f\left( x \right)={{e}^{x}}\), biết \(F\left( 0 \right)=4\). Tìm \(F\left( x \right)\).
-
Gieo một con xúc xắc cân đối đồng chất. Tính xác suất hiện mặt có số chấm là chẵn.
-
Cho \(f,\,\,g\) là hai hàm liên tục trên \(\left[ 1;3 \right]\)thỏa mãn: \(\int\limits_{1}^{3}{\left[ f\left( x \right)+3g\left( x \right) \right]dx=10}\) và \(\int\limits_{1}^{3}{\left[ 2f\left( x \right)-g\left( x \right) \right]dx}=6\). Tính \(\int\limits_{1}^{3}{\left[ f\left( x \right)+g\left( x \right) \right]dx}\).
-
Giá trị của giới hạn \(\underset{x\to 2}{\mathop{\lim }}\,\left( {{x}^{2}}+1 \right)\) là:
