Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng \(R\sqrt{3}\). Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho khoảng cách giữa AB và truc của hình trụ bằng \(\frac{R\sqrt{3}}{2}\). Góc giữa AB và trục của hình trụ bằng:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai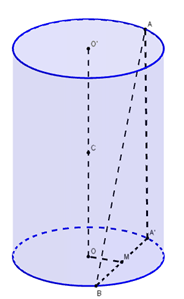
Gọi A’ là hình chiếu của A lên mặt đáy còn lại; M là trung điểm của A’B.
\(\Rightarrow AA'//OO',\,\,\,\,\,OM\bot A'B\)
\(\Rightarrow \left( \widehat{OO';AB} \right)=\left( \widehat{AA';AB} \right)\)
Mặt khác, \(AA'//OO'\)\(\Rightarrow OO'//(AA'B)\)
\(\Rightarrow d\left( OO';AB \right)=d\left( OO';(AA'B) \right)=d\left( O;(AA'B) \right)\)
Ta có: \(\left\{ \begin{align} & OM\bot A'B \\ & OM\bot AA' \\\end{align} \right.\Rightarrow OM\bot (AA'B)\)
\(\Rightarrow d\left( OO';AB \right)=OM=\frac{R\sqrt{3}}{2}\)
\(\Delta OMB\) vuông tại M \(\Rightarrow BM=\sqrt{O{{B}^{2}}-O{{M}^{2}}}=\sqrt{{{R}^{2}}-{{\left( \frac{R\sqrt{3}}{2} \right)}^{2}}}=\frac{R}{2}\)
\(\Delta AA'B\) vuông tại A’
\(\begin{array}{l}
\Rightarrow \tan \widehat {A'AB} = \frac{{A'B}}{{AA'}} = \frac{{2.BM}}{{AA'}}\\
= \frac{{2.\frac{R}{2}}}{{R\sqrt 3 }} = \frac{1}{{\sqrt 3 }}\\
\Rightarrow \widehat {A'AB} = {30^0}\\
\Rightarrow \left( {\widehat {OO';AB}} \right) = \left( {\widehat {AA';AB}} \right) = {30^0}
\end{array}\)
Chọn: A
Đề thi thử THPT QG năm 2023 môn Toán
Trường THPT Nguyễn Thị Diệu
Câu hỏi liên quan
-
Cho \(f(x)=a.\ln \left( x+\sqrt{{{x}^{2}}+1} \right)+b.{{x}^{2017}}+2018\) với \(a,b\in R\). Biết rằng \(f\left( \log \left( \log e \right) \right)=2019\). Tính giá trị của \(f\left( \log \left( \ln 10 \right) \right)\).
-
Tìm hệ số của \({{x}^{2}}\) trong khai triển \({{\left( 2x+\frac{1}{{{x}^{2}}} \right)}^{5}}\).
-
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với đáy. Gọi M là trung điểm AC. Khẳng định nào sau đây sai?
-
Cho hàm số \(f\left( x \right)\) có đạo hàm trên đoạn \(\left[ a;b \right]\) và \(f\left( a \right)=f\left( b \right)\). Hỏi mệnh đề nào sau đây đúng?
-
Cho hàm số \(y=f(x)\) có đạo hàm \(f'\left( x \right)=2018{{\left( x-1 \right)}^{2017}}{{\left( x-2 \right)}^{2018}}{{\left( x-3 \right)}^{2019}}\). Tìm số điểm cực trị của \(f(x)\).
-
Cho hàm số \(y=f(x)\) liên tục và có đạo hàm trên R thỏa mãn \(f(2)=-2,\,\,\int\limits_{0}^{2}{f\left( x \right)dx}=1\). Tính tích phân \(I=\int\limits_{0}^{4}{f'\left( \sqrt{x} \right)dx}\).
-
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau
.png)
Tìm tất cả các giá trị của m để phương trình \(f\left( x \right)=m\) có đúng 2 nghiệm.
-
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số \(y=\frac{x-3}{{{x}^{2}}-2mx+1}\) có 2 đường tiệm cận đứng.
-
Nếu \({{\left( 2-\sqrt{3} \right)}^{a-1}}<2+\sqrt{3}\) thì
-
Cho hàm số \(f(x)={{x}^{3}}+a{{x}^{2}}+bx-2\) thỏa mãn \(\left\{ \begin{array}{l}a + b > 1\\3 + 2a + b < 0\end{array} \right.\). Số điểm cực trị của hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) là:
-
Cho hình đa diện SABCD có \(SA=4,\,\,SB=2,\,\,SC=3,\,\,SD=1\) và \(\widehat{ASB}=\widehat{BSC}=\widehat{CSD}=\widehat{DSA}={{60}^{0}}\). Khoảng cách từ điểm A tới mặt phẳng \((SCD)\) là:
.png)
-
Số phức \(z=2-3i\) có số phức liên hợp là:
-
Tìm nguyên hàm \(I=\int{({{e}^{-x}}+2x)dx}\).
-
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa A’C’ và D’C là:
-
Cho dãy số \(\left( {{u}_{n}} \right)\) thỏa mãn \(\ln \left( {{u}_{3}}-4 \right)=\ln \left( 2{{u}_{n}}-4n+3 \right)\) với mọi \(n\in {{N}^{*}}\). Tính tổng \({{S}_{100}}={{u}_{1}}+{{u}_{2}}+...+{{u}_{100}}\).
-
Cho hàm số \(f(x)=\left| {{x}^{3}}-3{{x}^{2}}+m \right|\) với \(m\in \left[ -5;7 \right]\) là tham số. Có bao nhiêu giá trị nguyên của m để hàm số \(f\left( x \right)\) có đúng 3 điểm cực trị?
-
Giả sử \(F(x)\) là một nguyên hàm của hàm số \(f\left( x \right)={{e}^{x}}\), biết \(F\left( 0 \right)=4\). Tìm \(F\left( x \right)\).
-
Hàm số \(y={{\sin }^{4}}x+{{\cos }^{4}}x\) có tập giá trị \(T=\left[ a;b \right]\). Giá trị \(b-a\) là:
-
Số đường tiệm cận của đồ thị hàm số \(y=\frac{2x-1}{x+3}\) bằng:
-
Có 2 kiểu đồng hồ đeo tay (vuông, tròn) và 3 kiểu dây (kim loại, da, nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?
