Cho hàm số \(y={{x}^{3}}-6{{x}^{2}}+9x+m\text{ }\left( C \right)\), với \(m\) là tham số. Giả sử đồ thị \(\left( C \right)\) cắt trục hoành tại ba điểm phân biệt có hoành độ thỏa mãn \({{x}_{1}}<{{x}_{2}}<{{x}_{3}}\). Khẳng định nào sau đây đúng?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn C
Phương trình hoành độ giao điểm của đồ thị (C) với trục hoành \({{x}^{3}}-6{{x}^{2}}+9x+m=0\Leftrightarrow m=-{{x}^{3}}+6{{x}^{2}}-9x\) (1). Xét hàm số \(f\left( x \right)=-{{x}^{3}}+6{{x}^{2}}-9x\) với \(x\in \mathbb{R}\).
Ta có \(f'\left( x \right)=-3{{x}^{2}}+12x-9=0\)\(\Leftrightarrow \left[ \begin{align} & x=1 \\ & x=3 \\ \end{align} \right.\).
Ta có \(f\left( x \right)=0\Leftrightarrow -{{x}^{3}}+6{{x}^{2}}-9x=0\)
\(\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=3 \\ \end{align} \right.\)
và
\(f\left( x \right)=-4\\\Leftrightarrow -{{x}^{3}}+6{{x}^{2}}-9x=-4\\\Leftrightarrow \left[ \begin{align} & x=1 \\ & x=4 \\ \end{align} \right.\)
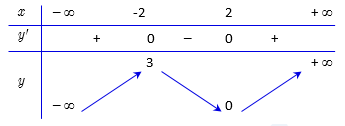
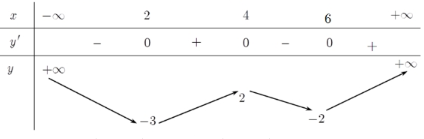
.BBT của hàm số \(f\left( x \right)\)
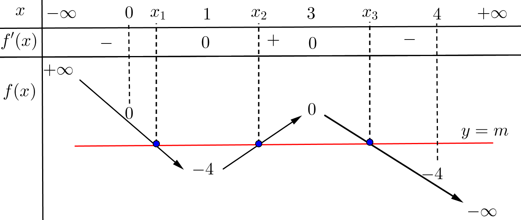
Đồ thị (C) cắt trục hoành tại 3 điểm phân biệt có hoành độ thoả mãn \({{x}_{1}}<{{x}_{2}}<{{x}_{3}}\)
\(\Leftrightarrow \) Phương trình (1) có 3 nghiệm \({{x}_{1}}<{{x}_{2}}<\,{{x}_{3}}\)
\(\Leftrightarrow \) Đường thẳng \(y=m\) cắt đồ thị hàm số \(f\left( x \right)\) tại 3 điểm có hoành độ \({{x}_{1}}<{{x}_{2}}<{{x}_{3}}\)
Dựa vào BBT ta suy ra \(0<{{x}_{1}}<1<{{x}_{2}}<3<{{x}_{3}}<4\).
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Sở GD&ĐT Bắc Ninh lần 1
Câu hỏi liên quan
-
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ?
-
Cho đồ thị \(\left( C \right):y=\frac{x+2}{x-1}\). Gọi \(A,\ B,\ C\) là ba điểm phân biệt thuộc \(\left( C \right)\) sao cho trực tâm \(H\)của tam giác \(ABC\) thuộc đường thẳng \(\Delta :y=-3x+10\). Độ dài đoạn thẳng \(OH\) bằng
-
Cho cấp số nhân \(\left( {{u}_{n}} \right)\) có \({{u}_{1}}=2\) và công bội \(q=-3\). Giá trị của \({{u}_{2}}\) bằng
-
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB=3,\,AD=4\) và các cạnh bên của hình chóp tạo với mặt đáy một góc \(60{}^\circ \). Tính thể tích khối cầu ngoại tiếp hình chóp đã cho.
-
Cho hai mặt phẳng \(\left( P \right)\)và \(\left( Q \right)\) song song với nhau và cùng cắt khối cầu tâm \(O\) bán kính \(4\sqrt{3}\) thành hai hình tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn này và có đáy là hình tròn còn lại. Khi diện tích xung quanh của hình nón là lớn nhất, khoảng cách \(h\) giữa hai mặt phẳng \(\left( P \right)\)và \(\left( Q \right)\) bằng:
-
Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số \(y=\frac{\sqrt{1-{{x}^{2}}}}{{{x}^{2}}+2x}\) là
-
Hình bát diện đều thuộc loại khối đa diện nào sau dây?
-
Mệnh đề nào dưới đây sai?
-
Nghiệm của phương trình \({{\left( \frac{1}{5} \right)}^{{{x}^{2}}-2x-3}}={{5}^{x+1}}\) là
-
Hàm số nào dưới đây không có cực trị?
-
Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\) có cạnh bằng \(a\). Gọi \(\alpha \)là góc giữa \(\left( AC{D}' \right)\) và \(\left( ABCD \right)\). Giá trị của \(\tan \alpha \) bằng:
-
Cho hình chóp \(S.ABC\) có \(AB=4a,BC=3\sqrt{2}a,\)\(\widehat{ABC}=45{}^\circ ;\widehat{SAC}=\widehat{SBC}=90{}^\circ \); Sin góc giữa hai mặt phẳng\(\left( SAB \right)\)và\(\left( SBC \right)\) bằng\(\frac{\sqrt{2}}{4}.\) Bán kính mặt cầu ngoại tiếp hình chóp đã cho bằng
-
Thể tích của khối chóp có diện tích đáy \(B=6\) và chiều cao \(h=4\) là
-
Cho khối chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a,\) cạnh bên \(SA=y\,\,\left( y>0 \right).\) và vuông góc với mặt phẳng đáy \(\left( ABCD \right)\). Trên cạnh \(AD\) lấy điểm \(M\) và đặt \(AM=x\,(0 < x < a).\) Tính thể tích lớn nhất \({{V}_{\max }}\) của khối chóp \(S.ABCM,\) biết \({{x}^{2}}+{{y}^{2}}={{a}^{2}}.\)
-
Cho khối lăng trụ \(ABC.{A}'{B}'{C}'\) có \(AB=3a,\)\(AC=4a,\) \(BC=5a,\)khoảng cách giữa hai đường thẳng \(AB\) và \({B}'{C}'\) bằng \(2a.\) Gọi \(M,\)\(N\) lần lượt là trung điểm của \({A}'{B}'\) và \({A}'{C}',\) (tham khảo hình vẽ dưới đây). Thể tích \(V\) của khối chóp \(A.BCNM\) là
-
Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y=\ln \left( {{x}^{2}}-2mx+4 \right)\) có tập xác định là \(\mathbb{R}.\)
-
Gọi \(n\) là số nguyên dương bất kì, \(n\ge 2\), công thức nào dưới đây đúng?
-
Lăng trụ tam giác \(ABC.A'B'C'\)có thể tích bằng \(V\). Khi đó, thể tích khối chóp \(A.AB{{C}^{'}}\) bằng:
-
Cho hàm số \(y=\frac{ax+b}{cx-1}\) có đồ thị như hình vẽ bên dưới. Giá trị của tổng \(S=a+b+c\) bằng:
-
Với các số \(a,\ b>0\) thỏa mãn \({{a}^{2}}+{{b}^{2}}=7ab\), biểu thức \({{\log }_{3}}\left( a+b \right)\) bằng
