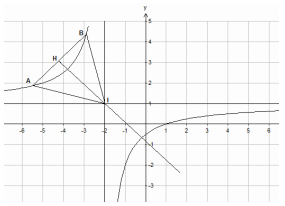
Cho hàm số \(y = \frac{{x - 1}}{{x + 2}}\) có đồ thị (C). Gọi I là giao điểm của hai tiệm cận của (C). Xét tam giác đều ABI có hai đỉnh A, B thuộc (C), đoạn thẳng AB có độ dài bằng:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTam giác \(IAB\) đều thì \(AB\) vuông góc với tia phân giác góc phần tử thứ \(II,IV\)
Phương trình \(AB:y = x + m\), phương trình hoành độ giao điểm của \(\left( C \right)\) và \(AB\) là :
\(\frac{{x - 1}}{{x + 2}} = x + m \Leftrightarrow {x^2} + \left( {m + 1} \right)x + 2m + 1 = 0\left( {x \ne - 2} \right)\)
Có \(\Delta = {m^2} - 6m - 3 > 0 \Leftrightarrow \left[ \begin{array}{l}m > 3 + 2\sqrt 3 \\m < 3 - 2\sqrt 3 \end{array} \right.\)
Tam giác \(ABI\) đều tại \(I\) khi và chỉ khi \(IH = \frac{{AB\sqrt 3 }}{2} \Leftrightarrow d\left( {I,AB} \right) = \frac{{AB\sqrt 3 }}{2}\)
\(\begin{array}{l} \Leftrightarrow \frac{{\left| {m - 3} \right|}}{{\sqrt 2 }} = \frac{{\sqrt 3 }}{2}.\sqrt 2 .\sqrt {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \\ \Leftrightarrow \left| {m - 3} \right| = \sqrt 3 .\sqrt {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \\ \Leftrightarrow {m^2} - 6m = 9\\ \Leftrightarrow AB = \sqrt {2\left( {{m^2} - 6m - 3} \right)} = 2\sqrt 3 \end{array}\)
Chọn B.
Đề thi thử THPT QG năm 2023 môn Toán
Trường THPT Chu Văn An
Câu hỏi liên quan
-
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{{x + 2}}{{x + 5m}}\) đồng biến trên khoảng \(\left( { - \infty ; - 10} \right)\)?
-
Trong hòm có 10 quả cầu có hình dạng và kích thước giống nhau, trong đó có 2 quả cầu trắng, 5 quả cầu xanh và 3 quả cầu vàng. Xác suất để khi lấy ngẫu nhiên 6 quả cầu thì có không quá 1 quả cầu trắng là bao nhiêu?
-
Cho khối chóp có đáy là hình vuông cạnh a và chiều cao bằng 2a. Thể tích của khối chóp đã cho bằng
-
Diện tích của mặt cầu bán kính R bằng
-
Số vị trí điểm biểu diễn các nghiệm của phương trình \(\frac{{\sin 2x + 2\cos x - \sin x - 1}}{{\tan x + \sqrt 3 }} = 0\) trên đường tròn lượng giác là bao nhiêu?
-
Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm \(34\) học sinh?
-
Trong không gian Oxyz, đường thẳng \(d:\left\{ \begin{array}{l}x = 2 - t\\y = 1 + 2t\\z = 3 + t\end{array} \right.\) có một vectơ chỉ phương là:
-
Cho khối lăng trụ ABC.A’B’C’, khoảng cách từ C đến đường thẳng BB’ bằng 2, khoảng cách từ A đến các đường thẳng BB’ và CC’ lần lượt bằng \(1\) và \(\sqrt 3 \), hình chiếu vuông góc của A lên mặt phẳng (A’B’C’) là trung điểm M của B’C’ và \(A'M = \frac{{2\sqrt 3 }}{3}\). Thể tích của khối lăng trụ đã cho bằng:
-
Ông \(A\) dự định sử dụng hết \(6,5{m^3}\) kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
-
Cho hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + d(a,b,c,d \in \mathbb{R})\) . Đồ thị của hàm số \(y = f(x)\) như hình vẽ bên.Số nghiệm thực của phương trình \(3f\left( x \right) + 4 = 0\) là:
.
.png)
-
Gọi S là diện tích của hình phẳng giới hạn bởi các đường thẳng \(y = {e^x},y = 0,x = 0,x = 2\). Mệnh đề nào dưới đây đúng ?
-
Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B, AB=a, SA vuông góc với mặt phẳng đáy và SA = 2a. Khoảng cách từ A đến mặt phẳng (SBC) bằng:
-
Cho \(a > 0,b > 0\) thỏa mãn \({\log _{3a + 2b + 1}}\left( {9{a^2} + {b^2} + 1} \right) + {\log _{6ab + 1}}\left( {3a + 2b + 1} \right) = 2\). Giá trị của \(a + 2b\) bằng:
-
Một người gửi tiết kiệm vào một ngân hàng với lãi suất \(7,5\% \)/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó thu được ( cả số tiền gửi ban đầu và lãi) gấp đôi số tiền gửi ban đầu, giả định trong khoảng thời gian này lãi suất không thay đổi và người đó không rút tiền ra ?
-
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và \(SB = 2a\). Góc giữa đường thẳng SB và mặt phẳng đáy bằng
-
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d(a,b,c,d \in \mathbb{R})\) có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là:
-
Với \(\alpha \) là số thực dương tùy ý, \(\ln \left( {5a} \right) - \ln \left( {3a} \right)\) bằng:
-
Số phức \( - 3 + 7i\) có phần ảo bằng:
-
Trong không gian Oxyz, cho hai điểm \(A\left( {2; - 4;3} \right)\) và \(B\left( {2;2;7} \right)\). Trung điểm của đoạn thẳng \(AB\) có tọa độ là:
-
Cho hình lập phương \(ABCD.A'B'C'D'\) có tâm \(O\). Gọi \(I\) là tâm của hình vuông \(A'B'C'D'\) và \(M\) là điểm thuộc đoạn thẳng \(OI\) sao cho \(MO = 2MI\) (tham khảo hình vẽ). Khi đó côsin của góc tạo bởi hai mặt phẳng \(\left( {MC'D'} \right)\) và \(\left( {MAB} \right)\) bằng:
.png)
