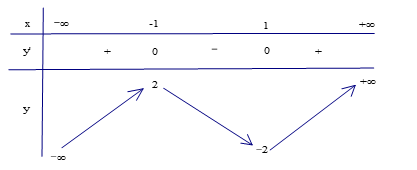
Cho hàm số \(f\left( x \right)=a{{x}^{4}}+b{{x}^{2}}+c\) có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên thuộc đoạn \(\left[ -2;5 \right]\) của tham số \(m\) để phương trình \(f\left( x \right)=m\) có đúng hai nghiệm phân biệt?

Cho tứ diện \(ABCD.\) Gọi \(G\) là trọng tâm tam giác \(BCD.\) Cặp đường thẳng nào sau đây cắt nhau?

Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có tất cả các cạnh bằng nhau. Góc giữa hai đường thẳng \(A{B}'\) và \(C{C}'\) bằng

Cho hình chóp \(S.ABC\)có \(SA=a\) và \(SA\) vuông góc với đáy. Biết đáy là tam giác vuông cân tại \(A\) và \(BC=a\sqrt{2}\). Tính khoảng cách từ \(A\) đến mặt phẳng \(\left( SBC \right)\).

Tiệm cận ngang của đồ thị hàm số \(y=\frac{2x-1}{2x+4}\) là đường thẳng có phương trình:

Nghiệm của phương trình \({{\log }_{3}}\left( 2x+1 \right)=1+{{\log }_{3}}\left( x-1 \right)\) là

Cho hai đường thẳng chéo nhau \(a\) và \(b\). Lấy hai điểm \(A,B\) phân biệt thuộc \(a\) và hai điểm \(C,D\) phân biệt thuộc \(b\). Khi đó hai đường thẳng \(A\text{D}\) và \(BC\) ở vị trí

Cho hai tích phân \(\int\limits_{-2}^{5}{f\left( x \right)\text{d}}x=8\) và \(\int\limits_{5}^{-2}{g\left( x \right)\text{d}}x=3\). Tính \(I=\int\limits_{-2}^{5}{\left[ f\left( x \right)-4g\left( x \right)-1 \right]\text{d}}x\)

Trong không gian Oxyz, cho mặt cầu \(\left( S \right):\,{{\left( x-2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=16\) và điểm \(A\left( -1;-1;-1 \right).\) Xét các điểm M thuộc \(\left( S \right)\)sao cho đường thẳng AM tiếp xúc với \(\left( S \right).\) M luôn thuộc một mặt phẳng cố định có phương trình là

Hàm số nào dưới đây có bảng biến thiên như sau:

Đạo hàm của hàm số \(y={{8}^{x}}\) là

Đặt \(a={{\log }_{2}}5,\,b={{\log }_{3}}5\). Hãy biểu diễn \({{\log }_{6}}5\)theo \(a\) và \(b\).

Có bao nhiêu số có năm chữ số khác nhau được tạo thành từ các chữ số 1,2,3,4,5,6?

Cho hai số phức \({{z}_{1}}=2+i,{{z}_{2}}=1-2i.\) Môđun của số phức \(w=\frac{z_{1}^{2022}}{z_{2}^{2023}}\) là

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA=a\) và \(SA\) vuông góc với mặt phẳng đáy. Thể tích khối chóp \(S.ABCD\) bằng

Cho hình trụ có bán kính đáy \(r\) và độ dài đường sinh \(l\). Diện tích xung quanh \({{S}_{xq}}\) của hình trụ đã cho được tính theo công thức nào dưới đây?

Trong không gian \(Oxyz\), mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=25\) có tọa độ tâm \(I\) và bán kính \(R\) là

Số giao điểm của đồ thị \((C):y={{x}^{3}}-3{{x}^{2}}+2x+1\) và đường thẳng \(y=1\) là

Cho hình nón đỉnh\(S\), đáy là đường tròn \(\left( O;\,5 \right)\).Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm \(A\) và \(B\) sao cho \(SA=AB=8\). Tính khoảng cách từ \(O\) đến \(\left( SAB \right)\).

Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ -1;1 \right\}\), thỏa mãn \(f'\left( x \right)=\frac{2}{{{x}^{2}}-1};\ f\left( -3 \right)+f\left( 3 \right)=2\ln 2\) và \(f\left( -\frac{1}{2} \right)+f\left( \frac{1}{2} \right)=0\). Giá trị của biểu thức \(P=f\left( -2 \right)+f\left( 0 \right)+f\left( 4 \right)\) là:

Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông cân tại \(C\) và \(SA\) vuông góc với mặt phẳng đáy. Cho \(SC=a\), mặt phẳng \(\left( SBC \right)\) tạo với mặt đáy một góc \(\alpha \). Thể tích khối chóp \(S.ABC\) đạt giá trị lớn nhất là