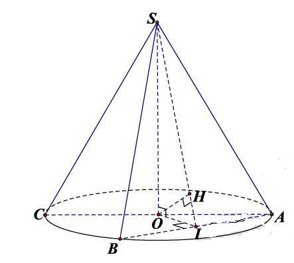
Cho hình nón đỉnh\(S\), đáy là đường tròn \(\left( O;\,5 \right)\).Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm \(A\) và \(B\) sao cho \(SA=AB=8\). Tính khoảng cách từ \(O\) đến \(\left( SAB \right)\).
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn B
Gọi \(I\) là trung điểm \(AB\).
Ta có
\(\left\{ \begin{align} & AB\bot SO \\ & AB\bot OI \\ \end{align} \right.\Rightarrow AB\bot \left( SOI \right)\\\Rightarrow \left( SAB \right)\bot \left( SOI \right)\)
Trong \(\left( SOI \right)\), kẻ \(OH\bot SI\) thì \(OH\bot \left( SAB \right)\).
\(\Rightarrow d\left( O;\,\left( SAB \right) \right)=OH\).
Ta có: \(SO=\sqrt{S{{A}^{2}}-O{{A}^{2}}}\)\( =\sqrt{{{\left( \frac{8.5}{5} \right)}^{2}}-{{5}^{2}}}=\sqrt{39}\).
Ta có: \(OI=\sqrt{O{{A}^{2}}-A{{I}^{2}}}\)\( =\sqrt{{{5}^{2}}-{{\left( \frac{4.5}{5} \right)}^{2}}}=3\).
Tam giác vuông \(SOI\) có: \(\frac{1}{O{{H}^{2}}}=\frac{1}{O{{I}^{2}}}+\frac{1}{SO{}^{2}}\)\( \Rightarrow OH=\frac{3\sqrt{13}}{4}\).
Vậy \(d\left( O;\,\left( SAB \right) \right)=OH=\frac{3\sqrt{13}}{4}\).
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Phú Lâm
Câu hỏi liên quan
-
Có bao nhiêu số có năm chữ số khác nhau được tạo thành từ các chữ số 1,2,3,4,5,6?
-
Cho hàm số bậc ba \(y=f\left( x \right)\) có đồ thị như hình vẽ, biết \(f\left( x \right)\) đạt cực tiểu tại điểm \(x=1\) và thỏa mãn \(\left[ f\left( x \right)+1 \right]\) và \(\left[ f\left( x \right)-1 \right]\) lần lượt chia hết cho \({{\left( x-1 \right)}^{2}}\) và \({{\left( x+1 \right)}^{2}}\). Gọi \({{S}_{1}},{{S}_{2}}\) lần lượt là diện tích như trong hình bên. Tính \(2{{S}_{2}}+8{{S}_{1}}\).
-
Gọi \({{z}_{1}}\) là nghiệm phức có phần ảo âm của phương trình \({{z}^{2}}-2z+5=0\). Tọa độ điểm biểu diễn số phức \(\frac{7-4i}{{{z}_{1}}}\) trên mặt phẳng phức là
-
Tiệm cận ngang của đồ thị hàm số \(y=\frac{2x-1}{2x+4}\) là đường thẳng có phương trình:
-
Cho điểm \(M\left( 1,-4,-2 \right)\) và mặt phẳng \(\left( P \right):x+y+5z-14=0\). Tính khoảng cách từ \(M\) đến \((P)\).
-
Cho số phức \(z=-1-2\sqrt{6}i\). Phần thực và phần ảo của số phức \(\overline{z}\) là?
-
Tập nghiệm của bất phương trình \(({{3}^{2x}}-9)({{3}^{x}}-\frac{1}{27})\sqrt{{{3}^{x+1}}-1}\le 0\) chứa bao nhiêu số nguyên ?
-
Cho \(F(x)\) là một nguyên hàm của hàm số \(f(x)\). Tìm \(I=\int{\left[ 2f(x)+1 \right]}\text{d}x\).
-
Thể tích của khối lăng trụ có diện tích đáy \(S=2{{a}^{2}}\), chiều cao \(h=6a\) là:
-
Cho hai số phức \({{z}_{1}}=2+i,{{z}_{2}}=1-2i.\) Môđun của số phức \(w=\frac{z_{1}^{2022}}{z_{2}^{2023}}\) là
-
Khẳng định nào sau đây đúng?
-
Cho tứ diện \(ABCD.\) Gọi \(G\) là trọng tâm tam giác \(BCD.\) Cặp đường thẳng nào sau đây cắt nhau?
-
Trong không gian \(Oxyz\), mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=25\) có tọa độ tâm \(I\) và bán kính \(R\) là
-
Trong không gian \(\text{Ox}yz\), đường thẳng \(d:\,\frac{x-1}{1}=\frac{y-3}{3}=\frac{z+4}{-2}\) đi qua điểm nào dưới đây?
-
Phương trình tiếp tuyến của đường cong \(y={{x}^{3}}+3{{x}^{2}}-2\) tại điểm có hoành độ \({{x}_{0}}=1\) là
-
Cho hai đường thẳng phân biệt \(a\) và \(b\) trong không gian. Có bao nhiêu vị trí tương đối giữa \(a\) và \(b\)?
-
Cho hàm số \(f\left( x \right)\) có đạo hàm\(f'\left( x \right)=x\left( x-1 \right){{\left( x+4 \right)}^{2023}},\,\forall x\in \mathbb{R}\) . Số điểm cực trị của hàm số đã cho là
-
Cho hình chóp \(S.ABC\)có \(SA=a\) và \(SA\) vuông góc với đáy. Biết đáy là tam giác vuông cân tại \(A\) và \(BC=a\sqrt{2}\). Tính khoảng cách từ \(A\) đến mặt phẳng \(\left( SBC \right)\).
-
Hàm số nào dưới đây có bảng biến thiên như sau:
-
Tập nghiệm của bất phương trình \({{3}^{{{x}^{2}}-13}}<27\) là
