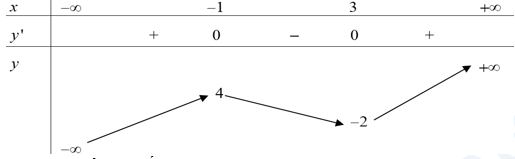
Cho hàm số bậc bốn \(y=f\left( x \right)\). Hàm số \(y={f}'\left( x \right)\) có đồ thị như hình vẽ sau

Hàm số \(y=f\left( x \right)\) nghịch biến trên khoảng nào trong các khoảng sau?

Cho số phức \(z=3+5i\), phần ảo của số phức \({{\bar{z}}^{2}}\) bằng

Trong không gian \(Oxyz\), cho ba điểm \(A\left( 3\,;-1\,\,;2 \right)\), \(B\left( 0\,;\,1\,;\,3 \right)\) và \(C\left( -1;\,1\,;1 \right)\). Đường thẳng đi qua \(C\) và song song với đường thẳng \(AB\) có phương trình là:

Trong không gian \(Oxyz\), cho hai mặt cầu \(\left( S \right):\,\,{{\left( x-3 \right)}^{2}}+{{y}^{2}}+{{z}^{2}}=9\) và \(\left( S' \right):\,\,{{\left( x+2 \right)}^{2}}+{{y}^{2}}+{{z}^{2}}=4\). Khẳng định nào sau đây là đúng?

Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có đáy là tam giác vuông cân đỉnh \(A\), mặt bên là \(BC{C}'{B}'\) hình vuông, khoảng cách giữa \(A{B}'\) và \(C{C}'\) bằng \(a\). Thể tích khối lăng trụ \(ABC.{A}'{B}'{C}'\) là

Kết quả thu gọn biểu thức \(P=\ln \left( 4x \right)-\ln \left( 2x \right)\) là

Tích các nghiệm của phương trình\(\log _{2}^{2}x-3{{\log }_{2}}x+2=0\)là

Diện tích xung quanh của hình nón có bán kính đáy \(r=5cm\)và độ dài đường sinh \(l=7cm\) bằng

Có bao nhiêu số nguyên \(x\) thỏa mãn \(\text{lo}{{\text{g}}_{3}}\frac{{{x}^{2}}-9}{125}\le \text{lo}{{\text{g}}_{5}}\frac{{{x}^{2}}-9}{27}\)?

Tập nghiệm của bất phương trình \(lo{{g}_{2}}\left( x+1 \right)<3\) là

Tiệm cận đứng của đồ thị hàm số \(y=\frac{x-1}{x-3}\) là đường thẳng có phương trình

Giả sử \(D\) là hình phẳng giới hạn bởi đường parabol \(y={{x}^{2}}-3x+2\) và trục hoành. Quay \(D\) quanh trục hoành ta thu được khối tròn xoay có thể tích bằng

Trong không gian với hệ trục tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right)\) có phương trình \(x+2y-3z-2=0\). Điểm nào sau đây thuộc mặt phẳng \(\left( P \right)\)?

Thầy Bình đặt lên bàn \(30\) tấm thẻ đánh số từ \(1\) đến \(30\). Bạn An chọn ngẫu nhiên \(10\) tấm thẻ. Tính xác suất để trong \(10\) tấm thẻ lấy ra có \(5\) tấm thẻ mang số lẻ, \(5\) tấm mang số chẵn trong đó chỉ có một tấm thẻ mang số chia hết cho \(10\).

Cho tập hợp \(M=\left\{ 1;2;3;4;5 \right\}\). Số tập con gồm hai phần tử của tập hợp \(M\) là:

Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( 0 \right)=0\) và \({f}'\left( x \right)\left( 1+{{e}^{f\left( x \right)}} \right)=1+{{e}^{x}},\forall x\in \mathbb{R}.\) Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=1,x=3.\)

Cho cấp số cộng \(\left( {{u}_{n}} \right)\) có \({{u}_{1}}=3\) và \({{u}_{2}}=-1\). Công sai của cấp số cộng đó bằng

Trên khoảng \(\left( 0;+\infty  \right)\), đạo hàm của hàm số \(y={{x}^{e}}\) là

Cho khối lăng trụ đứng có chiều cao bằng \(3\) và đáy là tam giác đều có độ dài cạnh bằng 2. Tính thể tích khối lăng trụ đã cho

Cho hình trụ có bán kính \(R\) và chiều cao \(\sqrt{3}R\). Hai điểm \(A\), \(B\) lần lượt nằm trên hai đường tròn đáy sao cho góc giữa \(AB\) và trục \(d\) của hình trụ bằng \(30{}^\circ \). Tính khoảng cách giữa \(AB\) và trục của hình trụ.

Cho hàm số \(y=f(x)\) có bảng biến thiên như sau

Giá trị cực đại của hàm số đã cho là