Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(3 \sqrt{x-1}+m \sqrt{x+1}=2 \sqrt[4]{x^{2}-1}\) có hai nghiệm thực?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐK \(x \geq 1\)
\(P t \Leftrightarrow 3 \frac{\sqrt{x-1}}{\sqrt{x+1}}+m=2 \frac{\sqrt[4]{x^{2}-1}}{\sqrt[4]{(x+1)^{2}}} \Leftrightarrow 3 \sqrt{\frac{x-1}{x+1}}+m=2 \sqrt[4]{\frac{x-1}{x+1}}\)
Đặt \(t=\sqrt[4]{\frac{x-1}{x+1}} \text { với } x \geq 1 \text { ta có } 0 \leq t<1\)
Thay vào phương trình ta được \(m=2 t-3 t^{2}=f(t)\)
\(f^{\prime}(t)=2-6 t \text { ta có: } f^{\prime}(t)=0 \Leftrightarrow t=\frac{1}{3}\)
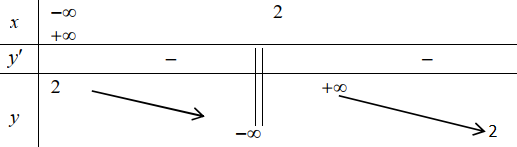
Bảng biến thiên
Từ bảng biến thiên ta có để phương trình có hai nghiệm khi \(0 \leq m<\frac{1}{3}\)
Câu hỏi liên quan
-
Cho hàm số y=f(x) có bảng biến thiên như hĩnh vẽ.
Hỏi phương trình \(|f(x+2017)-2018|=2019\) có bao nhiêu nghiệm?
-
Cho hàm số \(y=2{x^3} - 3\left( {m + 1} \right){x^2} + 6\left( {m + 1} \right)2x + 1\). Hình nào dưới đây mô tả chính xác nhất đồ thị hàm số trên?
-
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
-
Cho hàm số \(y = \sqrt {2 - {x^2}} .\) Gọi M và mm lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Khi đó M − 2m bằng
-
Xác định giá trị của tham số \(m\) để hàm số \(y = {x^3} - 3\left( {m - 1} \right){x^2} - 3\left( {m + 1} \right)x - 5\) có cực trị.
-
Cho hàm số \(y = – 2{x^3} + 3{x^2} – 1\) có đồ thị \(\left( C \right)\) như hình vẽ. Dùng đồ thị \(\left( C \right)\) suy ra tất cả giá trị tham số m để phương trình \(2{x^3} – 3{x^2} + 2m = 0\left( 1 \right)\) có ba nghiệm phân biệt là
.jpg.png)
-
Hàm số \(y=\frac{x-2}{x-1}\) có đồ thị là hình vẽ nào sau đây?
-
Đường cong trong hình vẽ sau đây là đồ thị của hàm số nào?
-
Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số \(y\; = \;\frac{x}{{\left| {x\; - \;1} \right|}}\) ?
-
Cho hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaa % dIhacqGHRaWkcaaIXaaabaGaamiEaiabgkHiTiaaigdaaaaaaa!4024! y = \frac{{{x^2} - x + 1}}{{x - 1}}\) có đồ thị (C). Gọi A,B là hai điểm phân biệt trên đồ thị (C) có hoành độ \(x_1;x_2\) thỏa \(x_1<1<x_2\). Giá trị nhỏ nhất của AB là
-
Cho hàm số \(y = (x – 2)\left( {{x^2} + mx + {m^2} – 3} \right)\). Tất cả giá trị của tham số m để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt là
-
Cho hàm số f(x) = x3-3x2+ 2 có đồ thị là đường cong trong hình bên. Tìm tất cả các giá trị thực của tham số m đề phương trình |x|3−3x2+2 = mx3-3x2+2 = m có nhiều nghiệm thực nhất
-
Cho hàm số y = f(x) xác định trên R và có đồ thị như hình bên. Hỏi phương trình f(|x-2|) = \(\frac{{ - 1}}{2}\) có bao nhiêu nghiệm?
-
Đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaG4maiaadIhacqGHsislcaaIXaaabaGaaGOmaiaa % dIhacqGHRaWkcaaIXaaaaaaa!3EC0! y = \frac{{3x - 1}}{{2x + 1}}\) có tâm đối xứng là điểm.
-
Giao điểm của đồ thị hàm số \(y = \dfrac{{2x + 1}}{{2x - 1}}\) với đường thẳng y = x + 2 là:
-
Cho hàm số y=f(x) có đồ thị như hình vẽ.
Tìm số nghiệm thuộc \(\left[-\frac{\pi}{6} ; \frac{5 \pi}{6}\right]\) của phương trình \(f(2 \sin x+2)=1 ?\)
-
Hàm số nào sau đây có bảng biến thiên như hình bên?
-
Cho hàm số \(y = \frac{{mx - 1}}{{x + 2}}\) có đồ thị là (C) . Tìm m để đường thẳng d: y = 2x-1 cắt đồ thị (C) tại hai điểm phân biệt A; B sao cho AB = \(\sqrt {10} \)
-
Tìm tập hợp tất cả các giá trị của tham số m sao cho bất phương trình sau có nghiệm:\(\sqrt{x+5}+\sqrt{4-x} \geq m\)
-
Hàm số y = f(x) xác định, liên tục trên khoảng K và có đạo hàm f′(x) trên K. Biết hình vẽ sau đây là của đồ thị hàm số f′(x) trên K.
.png)
Khẳng định nào sau đây là đúng?
