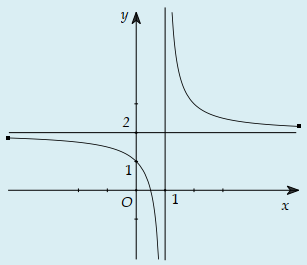
Cho hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaa % dIhacqGHRaWkcaaIXaaabaGaamiEaiabgkHiTiaaigdaaaaaaa!4024! y = \frac{{{x^2} - x + 1}}{{x - 1}}\) có đồ thị (C). Gọi A,B là hai điểm phân biệt trên đồ thị (C) có hoành độ \(x_1;x_2\) thỏa \(x_1<1<x_2\). Giá trị nhỏ nhất của AB là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaa % dIhacqGHRaWkcaaIXaaabaGaamiEaiabgkHiTiaaigdaaaGaeyypa0 % JaamiEaiabgUcaRmaalaaabaGaaGymaaqaaiaadIhacqGHsislcaaI % Xaaaaaaa!4679! y = \frac{{{x^2} - x + 1}}{{x - 1}} = x + \frac{1}{{x - 1}}\). Giả sử \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaabm % aabaGaamiEamaaBaaaleaacaaIXaaabeaakiaacUdacaaMc8UaaGPa % VlaadIhadaWgaaWcbaGaaGymaaqabaGccqGHRaWkdaWcaaqaaiaaig % daaeaacaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaeyOeI0IaaGymaaaa % aiaawIcacaGLPaaaaaa!4537! A\left( {{x_1};\,\,{x_1} + \frac{1}{{{x_1} - 1}}} \right)\), \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqamaabm % aabaGaamiEamaaBaaaleaacaaIYaaabeaakiaacUdacaaMc8UaaGPa % VlaadIhadaWgaaWcbaGaaGOmaaqabaGccqGHRaWkdaWcaaqaaiaaig % daaeaacaWG4bWaaSbaaSqaaiaaikdaaeqaaOGaeyOeI0IaaGymaaaa % aiaawIcacaGLPaaaaaa!453B! B\left( {{x_2};\,\,{x_2} + \frac{1}{{{x_2} - 1}}} \right)\) với \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBa % aaleaacaaIXaaabeaakiabgYda8iaaigdacqGH8aapcaWG4bWaaSba % aSqaaiaaikdaaeqaaaaa!3C8A! {x_1} < 1 < {x_2}\)
Đặt \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaqaabe % qaaiaadIhadaWgaaWcbaGaaGymaaqabaGccqGH9aqpcaaIXaGaeyOe % I0IaamyyaiaaykW7daqadaqaaiaadggacqGH+aGpcaaIWaaacaGLOa % GaayzkaaaabaGaamiEamaaBaaaleaacaaIYaaabeaakiabg2da9iaa % igdacqGHRaWkcaWGIbWaaeWaaeaacaWGIbGaeyOpa4JaaGimaaGaay % jkaiaawMcaaaaacaGL7baacqGHshI3daGabaabaeqabaGaamyEamaa % BaaaleaacaaIXaaabeaakiabg2da9iaaigdacqGHsislcaWGHbGaey % OeI0YaaSaaaeaacaaIXaaabaGaamyyaaaaaeaacaWG5bWaaSbaaSqa % aiaaikdaaeqaaOGaeyypa0JaaGymaiabgUcaRiaadkgacqGHRaWkda % WcaaqaaiaaigdaaeaacaWGIbaaaaaacaGL7baacqGHshI3daWhcaqa % aiaadgeacaWGcbaacaGLxdcacqGH9aqpdaqadaqaaiaadkgacqGHRa % WkcaWGHbGaai4oaiaaykW7caWGIbGaey4kaSIaamyyaiabgUcaRmaa % laaabaGaaGymaaqaaiaadkgaaaGaey4kaSYaaSaaaeaacaaIXaaaba % GaamyyaaaaaiaawIcacaGLPaaaaaa!74A7! \left\{ \begin{array}{l} {x_1} = 1 - a\,\left( {a > 0} \right)\\ {x_2} = 1 + b\left( {b > 0} \right) \end{array} \right. \Rightarrow \left\{ \begin{array}{l} {y_1} = 1 - a - \frac{1}{a}\\ {y_2} = 1 + b + \frac{1}{b} \end{array} \right. \Rightarrow \overrightarrow {AB} = \left( {b + a;\,b + a + \frac{1}{b} + \frac{1}{a}} \right)\)
\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiaadk % eadaahaaWcbeqaaiaaikdaaaGccqGH9aqpdaqadaqaaiaadggacqGH % RaWkcaWGIbaacaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaOGaey % 4kaSYaaeWaaeaacaWGHbGaey4kaSIaamOyaiabgUcaRmaalaaabaGa % aGymaaqaaiaadggaaaGaey4kaSYaaSaaaeaacaaIXaaabaGaamOyaa % aaaiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaGccqGH9aqpdaqa % daqaaiaadggacqGHRaWkcaWGIbaacaGLOaGaayzkaaWaaWbaaSqabe % aacaaIYaaaaOWaaeWaaeaacaaIYaGaey4kaSYaaSaaaeaacaaIYaaa % baGaamyyaiaadkgaaaGaey4kaSYaaSaaaeaacaaIXaaabaGaamyyam % aaCaaaleqabaGaaGOmaaaakiaadkgadaahaaWcbeqaaiaaikdaaaaa % aaGccaGLOaGaayzkaaWaaCbiaeaacqGHLjYSaSqabeaaciGGdbGaai % 4BaiaacohacaWGPbaaaOGaaGinaiaadggacaWGIbWaaeWaaeaacaaI % YaGaey4kaSYaaSaaaeaacaaIYaaabaGaamyyaiaadkgaaaGaey4kaS % YaaSaaaeaacaaIXaaabaGaamyyamaaCaaaleqabaGaaGOmaaaakiaa % dkgadaahaaWcbeqaaiaaikdaaaaaaaGccaGLOaGaayzkaaaaaa!6E8F! A{B^2} = {\left( {a + b} \right)^2} + {\left( {a + b + \frac{1}{a} + \frac{1}{b}} \right)^2} = {\left( {a + b} \right)^2}\left( {2 + \frac{2}{{ab}} + \frac{1}{{{a^2}{b^2}}}} \right)\mathop \ge \limits^{{\mathop{\rm Cos}\nolimits} i} 4ab\left( {2 + \frac{2}{{ab}} + \frac{1}{{{a^2}{b^2}}}} \right)\)
\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0JaaG % ioaiaadggacaWGIbGaey4kaSYaaSaaaeaacaaI0aaabaGaamyyaiaa % dkgaaaGaey4kaSIaaGioamaaxacabaGaeyyzImlaleqabaGaci4qai % aac+gacaGGZbGaamyAaaaakiaaikdadaGcaaqaaiaaiIdacaWGHbGa % amOyaiaac6cadaWcaaqaaiaaisdaaeaacaWGHbGaamOyaaaaaSqaba % GccqGHRaWkcaaI4aGaeyypa0JaaGioamaakaaabaGaaGOmaaWcbeaa % kiabgUcaRiaaiIdaaaa!5112! = 8ab + \frac{4}{{ab}} + 8\mathop \ge \limits^{{\mathop{\rm Cos}\nolimits} i} 2\sqrt {8ab.\frac{4}{{ab}}} + 8 = 8\sqrt 2 + 8\)Vậy \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiaadk % eadaWgaaWcbaGaamyBaiaadMgacaWGUbaabeaakiabg2da9maakaaa % baGaaGioamaakaaabaGaaGOmaaWcbeaakiabgUcaRiaaiIdaaSqaba % aaaa!3EF2! A{B_{min}} = \sqrt {8\sqrt 2 + 8} \)



.jpg.png)