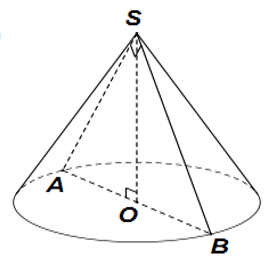
Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng \(a\sqrt2\) và góc giữa đường sinh và mặt phẳng đáy bằng 600. Diện tích xung quanh Sxq của hình nón và thể tích V của khối nón tương ứng là:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Gọi A là một điểm thuộc đường tròn đáy của hình nón.
Đường sinh \(SA=a\sqrt2\), góc giữa đường sinh và mặt phẳng đáy \( \widehat {SAO} = {60^0}\)
Tam giác SAO vuông tại O có:
\( OA = SA\cos {60^0} = \frac{{a\sqrt 2 }}{2};SO = SA\sin {60^0} = a\sqrt 2 .\frac{{\sqrt 3 }}{2} = \frac{{a\sqrt 6 }}{2}\)
Diện tích xung quanh hình nón:
\( {S_{xq}} = \pi rl = \pi .\frac{{a\sqrt 2 }}{2}.a\sqrt 2 = \pi {a^2}\)
Thể tích
\( V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi .{\left( {\frac{{a\sqrt 2 }}{2}} \right)^2}.\frac{{a\sqrt 6 }}{2} = \frac{{\pi {a^3}\sqrt 6 }}{{12}}\)
Câu hỏi liên quan
-
Hình nón có thiết diện cắt bởi mặt phẳng qua trục là một tam giác vuông và có diện tích xung quanh là \(\sqrt 2 \). Độ dài đường cao của hình nón là:
-
Diện tích xung quanh của hình nón có bán kính đường tròn đáy (R ) và chiều cao (h ) bằng:
-
Cho hình chữ nhật ABCD có AB = 3, AD = 4 quay xung xung quanh cạnh AB tạo ra một hình trụ. Thể tích của khối trụ đó là.
-
Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a. Diện tích xung quanh của hình nón bằng
-
Cho hình nón có bán kính đáy \(r = \sqrt 3\), độ dài đường sinh l = 4. Tính diện tích xung quanh của hình nón đó?
-
Cho hình chữ nhật ABCD có AC = 2AD = 2a. Quay quanh trục AB đường gấp khúc ADCB ta được hình trụ có diện tích xung quanh là:
-
Cho tam giác ABC vuông tại A, AB = 6, AC = 8. Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là
-
Cho hình nón có bán kính đáy \(r = \sqrt 3 \) và độ dài đường sinh \(l = 4\). Tính diện tích xung quanh của hình nón đã cho.
-
Cho \(AA'B'B\) là thiết diện song song với trục OO’ của hình trụ (A, B thuộc đường tròn tâm O). Cho biết \(AB=4,\text{AA }\!\!'\!\!\text{ =3}\) và thể tích của hình trụ bằng \(V=24\pi .\) Khoảng cách d từ O đến mặt phẳng \(\left( \text{AA}'B'B \right)\) là:
-
Cho hình trụ có bán kính đáy 10cm và đường cao là 15cm. ta để một thước thẳng có chiều dài l vào trong hình trụ. Khi đó trong các kết quả sau l có thể nhận giá trị lớn nhất là:
-
Nếu cắt mặt trụ bởi mặt phẳng vuông góc với trục ta được là:
-
Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a . Người ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chiều dài đường sinh bằng 2a thì bán kính đáy bằng:
-
Công thức tính thể tích khối nón biết diện tích đáy Sd và đường sinh l là:
-
Cho hình nón có các kích thước (r = 1;h = 2 ) với (r,h ) lần lượt là bán kính đáy và độ dài đường cao hình nón. Diện tích toàn phần hình nón là:
-
Cho hình nón có các kích thước r = 1cm;l = 2cm với r,l lần lượt là bán kính đáy và độ dài đường sinh hình nón. Diện tích toàn phần hình nón là:
-
Cho hình trụ có bán kính đáy bằng (1 ) và chiều cao bằng (3 ). Thiết diện của hình trụ cắt bởi mặt phẳng qua trục của nó có diện tích bằng:3
-
Chọn phát biểu đúng: Khi quay tam giác (ABC ) vuông tại (A ) quanh trục (AB ) thì
-
Một hình trụ có chu vi của đường tròn đáy \(4\pi a\) , chiều cao a. Thể tích khối trụ này bằng
-
Cho đường thẳng d cố định. Đường thẳng \(\Delta \) song song với d và cách d một khoảng không đổi. Xác định mặt tròn xoay tạo thành khi quay \(\Delta \) quanh d.
-
Cho a > b > 0. Đường elip (E) có phương trình \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1.\) Diện tích của hình elip (E) là
