ADMICRO
Cho hàm số \(y = f\left( x \right)\) xác định trên tập số thực \(\mathbb{R}\) và có đạo hàm \(f’\left( x \right) = \left( {x – \sin x} \right)\left( {x – m – 3} \right){\left( {x – \sqrt {9 – {m^2}} } \right)^3}\,\forall x\in \mathbb{R}\) (m là tham số). Có bao nhiêu giá trị nguyên của m để hàm số \(y = f\left( x \right)\) đạt cực tiểu tại x = 0?
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Môn: Toán Lớp 12
Bài: Cực trị của hàm số
ZUNIA12
Lời giải:
Báo saiĐiều kiện \(9 – {m^2} \ge 0 \Leftrightarrow – 3 \le m \le 3\)
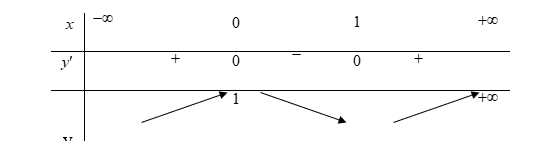
TH 1: \(0 \le m < 3\) ta có BTT
.png)
TH 2: \( – 3 \le m < 0\) ta có BTT
.png)
TH 2: m = 3 ta có BTT
.png)
Từ đó suy ra \( – 3 \le m < 3 \Rightarrow \) có 6 giá trị nguyên của m thỏa mãn.
ZUNIA9
AANETWORK