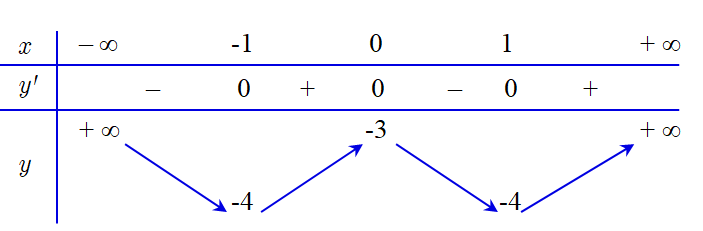
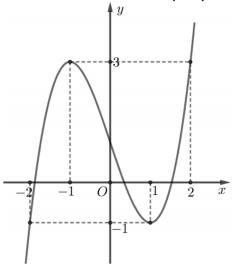
Biết rằng đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaiodaaaGccqGHRaWkcaaIZaGaamiE % amaaCaaaleqabaGaaGOmaaaaaaa!3D6E! y = {x^3} + 3{x^2}\) có dạng như hình vẽ:
.png)
Hỏi đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maaemaabaGaamiEamaaCaaaleqabaGaaG4maaaakiabgUcaRiaa % iodacaWG4bWaaWbaaSqabeaacaaIYaaaaaGccaGLhWUaayjcSdaaaa!409A! y = \left| {{x^3} + 3{x^2}} \right|\) có bao nhiêu điểm cực trị?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có:\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maaemaabaGaamiEamaaCaaaleqabaGaaG4maaaakiabgUcaRiaa % iodacaWG4bWaaWbaaSqabeaacaaIYaaaaaGccaGLhWUaayjcSdaaaa!409A! y = \left| {{x^3} + 3{x^2}} \right|\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0Zaai % qaaqaabeqaaiaadIhadaahaaWcbeqaaiaaiodaaaGccqGHRaWkcaaI % ZaGaamiEamaaCaaaleqabaGaaGOmaaaakiaaykW7caaMc8UaaGPaVl % aaykW7caaMc8UaaGPaVlaabUgacaqGObGaaeyAaiaaykW7caWG4bWa % aWbaaSqabeaacaaIZaaaaOGaey4kaSIaaG4maiaadIhadaahaaWcbe % qaaiaaikdaaaGccqGHLjYScaaIWaGaeyi1HSTaamiEaiabgwMiZkab % gkHiTiaaiodaaeaacqGHsislcaWG4bWaaWbaaSqabeaacaaIZaaaaO % GaeyOeI0IaaG4maiaadIhadaahaaWcbeqaaiaaikdaaaGccaaMc8Ua % aGPaVlaabccacaqGRbGaaeiAaiaabMgacaaMc8UaamiEamaaCaaale % qabaGaaG4maaaakiabgUcaRiaaiodacaWG4bWaaWbaaSqabeaacaaI % YaaaaOGaeyipaWJaaGimaiabgsDiBlaadIhacqGH8aapcqGHsislca % aIZaaaaiaawUhaaaaa!75BC! = \left\{ \begin{array}{l} {x^3} + 3{x^2}\,\,\,\,\,\,{\rm{khi}}\,{x^3} + 3{x^2} \ge 0 \Leftrightarrow x \ge - 3\\ - {x^3} - 3{x^2}\,\,{\rm{ khi}}\,{x^3} + 3{x^2} < 0 \Leftrightarrow x < - 3 \end{array} \right.\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0Zaai % qaaqaabeqaaiaadIhadaahaaWcbeqaaiaaiodaaaGccqGHRaWkcaaI % ZaGaamiEamaaCaaaleqabaGaaGOmaaaakiaaykW7caaMc8UaaGPaVl % aaykW7caaMc8UaaGPaVlaabUgacaqGObGaaeyAaiaaykW7caWG4bGa % eyyzImRaeyOeI0IaaG4maaqaaiabgkHiTiaadIhadaahaaWcbeqaai % aaiodaaaGccqGHsislcaaIZaGaamiEamaaCaaaleqabaGaaGOmaaaa % kiaaykW7caaMc8UaaeiiaiaabUgacaqGObGaaeyAaiaaykW7caWG4b % GaeyipaWJaeyOeI0IaaG4maaaacaGL7baaaaa!61C5! = \left\{ \begin{array}{l} {x^3} + 3{x^2}\,\,\,\,\,\,{\rm{khi}}\,x \ge - 3\\ - {x^3} - 3{x^2}\,\,{\rm{ khi}}\,x < - 3 \end{array} \right.\)
Nên ta lấy phần đối xứng của đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaiodaaaGccqGHRaWkcaaIZaGaamiE % amaaCaaaleqabaGaaGOmaaaaaaa!3D6E! y = {x^3} + 3{x^2}\) khi .x < -3
.png)
Dựa vào đồ thị, ta thấy đồ thị hàm số có 3 điểm cực trị.
Câu hỏi liên quan
-
Số điểm cực đại của hàm số \(f\left( x \right) = \frac{3}{4}{{\rm{x}}^4} + \frac{1}{2}{{\rm{x}}^2} - 1\) là
-
Tọa độ điểm cực đại của đồ thị hàm số \(y = – 2{x^3} + 3{x^2} + 1\) là:
-
Tìm các giá trị của tham số m để đồ thị hàm số: \(y=x^{4}-2(m+1) x^{2}+m^{2}\) có ba điểm cực trị là ba đỉnh của một tam giác vuông cân
-
Đồ thị của hàm số \(y = – {x^3} + 3{x^2} + 9x + 1\) có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB ?
-
Đồ thị hàm số \(y = {x^4} - 3{x^2} + 5\) có bao nhiêu điểm cực tiểu?
-
Cho hàm số y = x3-3x2. Tìm tất cả các giá trị thực tham số m để đường thẳng đi qua 2 điểm cực trị của đồ thị C tạo với đường thẳng x+ my+ 3 = 0 một góc α biết \(\cos \alpha = \frac{4}{5}\).
-
Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số \(y = - {x^3} + 3mx + 1\) có 2 điểm cực trị A, B sao cho tam giác OAB vuông tại O (với O là gốc tọa độ ).
-
Số cực trị của hàm số \(f\left( x \right) = \frac{3}{4}{{\rm{x}}^4} + \frac{1}{2}{{\rm{x}}^2} - 1\) là
-
Cho hàm số y=f(x) có đồ thị như hình bên dưới. Đồ thị hàm số \(g(x)=|f(x)+4|\) có tổng tung độ của các điểm cực trị bằng ?
.png)
-
Biết đồ thị hàm số \(y = {x^3}\; - 3x + 1\) có hai điểm cực trị A,B . Khi đó phương trình đường thẳng AB là
-
Cho hàm số y=f(x) có \(f'\left( x \right) = {\left( x - \frac{1}{2} \right)^2}{\left( {x + 3} \right)^{2021}}{\left( {2x - 5} \right)^2}x\). Điểm cực đại của hàm số là
-
Số điểm cực đại của đồ thị hàm số \(y = {x^4} + 100\) là
-
Điểm cực đại của đồ thị hàm số \(y = - {x^4} + 4{x^2} + 2\) là:
-
Điểm cực đại của hàm số \(y = \frac{1}{4}{x^4} - 2{x^2} + 5\) là:
-
Số cực trị của hàm số \(f\left( x \right) = - 5{{\rm{x}}^4}{\rm{ + }}{{\rm{x}}^2} + 7\) là
-
Số điểm cực trị của hàm số \(f\left( x \right) = – {x^4} + 2{x^2} – 3\) là
-
Cho hàm số \(y = f\left( x \right)\) liên tục và xác định trênvà có đồ thị như hình vẽ. Số giá trị nguyên của tham số m để hàm số \(y = \left| {{{\left( {f\left( x \right)} \right)}^2} + 2mf\left( x \right) + 2m + 35} \right|\) có đúng 3 điểm cực trị
.jpg.png)
-
Gọi M, n lần lượt là giá trị cực đại, giá trị cực tiểu của hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\). Khi đó giá trị của biểu thức M2−2n bằng
-
Cho hàm số \(y = \frac{{{x^2} - 2x}}{{13}}\). Khẳng định nào sau đây là đúng?
-
Số cực trị của hàm số \(f\left( x \right) = 3{{\rm{x}}^4}{\rm{ - 5}}{{\rm{x}}^2} - 3\) là
