Đề thi giữa HK1 môn Toán 8 năm 2022-2023
Trường THCS Lê Văn Tám
-
Câu 1:
Kết quả của phép tính \(\left( {a{x^2} + bx-c} \right).2{a^2}x\) bằng
A. 2a4x3 + 2a2bx2 – 2a2cx
B. 2a3x3 + bx – c
C. 2a4x2 + 2a2bx2 – a2cx
D. 2a3x3 + 2a2bx2 – 2a2cx
-
Câu 2:
Chọn câu sai.
A. Giá trị của biểu thức ax(ax + y) tại x = 1; y = 0 là a2.
B. Giá trị của biểu thức ay2(ax + y) tại x = 0; y = 1 là (1 + a)2.
C. Giá trị của biểu thức -xy(x - y) tại x = -5; y = -5 là 0.
D. Giá trị của biểu thức xy(-x - y) tại x = 5; y = -5 là 0.
-
Câu 3:
Cho biểu thức C = x(y + z) – y(z + x) – z(x – y). Chọn khẳng định đúng
A. Biểu thức C không phụ thuộc vào x; y; z
B. Biểu thức C phụ thuộc vào cả x; y; z
C. Biểu thức C chỉ phụ thuộc vào y
D. Biểu thức C chỉ phụ thuộc vào z
-
Câu 4:
Cho biểu thức A = x(x + 1) + (1 – x)(1 + x) – x. Khẳng định nào sau đây là đúng.
A. A = 2 – x
B. A < 1
C. A > 0
D. A > 2
-
Câu 5:
Cho biểu thức B = (2x – 3)(x + 7) – 2x(x + 5) – x. Khẳng định nào sau đây là đúng.
A. B = 21 – x
B. B < -1
C. B > 0
D. 10 < B < 20
-
Câu 6:
Cho A = (3x+7)(2x + 3) – (3x – 5)(2x + 11); B = x(2x + 1) – x2(x + 2) + x3 – x + 3. Chọn khẳng định đúng
A. A = B
B. A = 25B
C. A = 25B + 1
D. \(A = \frac{B}{2}\)
-
Câu 7:
Cho hình vẽ sau. Chọn câu sai.
.png)
A. Hai cạnh kề nhau: AB, BC
B. Hai cạnh đối nhau: BC, AD
C. Hai góc đối nhau: \(\widehat A\) và \(\widehat B\)
D. Các điểm nằm ngoài: H, E
-
Câu 8:
Các góc của tứ giác có thể là:
A. 4 góc nhọn
B. 4 góc tù
C. 1 góc vuông, 3 góc nhọn
D. 4 góc vuông
-
Câu 9:
Chọn câu đúng nhất trong các câu sau khi định nghĩa tứ giác ABCD:
A. Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA
B. Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA, trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng
C. Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA trong đó hai đoạn thẳng kề một đỉnh song song với nhau
D. Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA và 4 góc tại đỉnh bằng nhau
-
Câu 10:
Biểu thức \({\left( {a - b - c} \right)^2}\) bằng
A. a2 + b2 + c2 – 2(bc + ac + ab)
B. a2 + b2 + c2 + bc – ac – 2ab
C. a2 + b2 + c2 + 2(bc – ac – ab)
D. a2 + b2 + c2 + 2(bc – ac – ab)
-
Câu 11:
Khai triển \(4{x^2} - 25{y^2}\) theo hằng đẳng thức ta được
A. (4x – 5y)(4x + 5y)
B. (4x – 25y)(4x + 25y)
C. (2x – 5y)(2x + 5y)
D. (2x – 5y)2
-
Câu 12:
So sánh \(A = 2019.2021.a\) và \(B = \left( {{{2019}^2} + 2.2019 + 1} \right)a\) (với a > 0)
A. A = B
B. A ≥ B
C. A > B
D. A < B
-
Câu 13:
Hãy chọn câu sai.
A. Hình thang là tứ giác có hai cạnh đối song song.
B. Nếu hình thanh có hai cạnh bên song song thì tất cả các cạnh của hình thang bằng nhau.
C. Nếu một hình thang có hai cạnh đáy bằng nhau thị hai cạnh bên bằng nhau, hai cạnh bên song song.
D. Hình thang vuông là hình thang có một góc vuông.
-
Câu 14:
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB, AC lần lượt tại D và E. Chọn khẳng định đúng nhất?
A. Tứ giác BDIC là hình thang
B. Tứ giác BIEC là hình thang
C. Tứ giác BDEC là hình thang
D. Cả A, B, C đều đúng
-
Câu 15:
Cho tam giác ABC vuông tại A, đường cao AH. Trên BC lấy điểm M sao cho CM = CA. Đường thẳng đi qua M và song song với CA cắt AB tại I. Chọn câu đúng nhất. Tứ giác ACMI là hình gì?
A. Hình thang cân
B. Hình thang vuông
C. Hình thang
D. Đáp án khác
-
Câu 16:
Nhân tử chung của biểu thức \(30{\left( {4 - 2x} \right)^2} + 3x - 6\) có thể là
A. x + 2
B. 3(x – 2)
C. (x – 2)2
D. (x + 2)2
-
Câu 17:
Cho \(ab\left( {x - 5} \right) - {a^2}\left( {5 - x} \right) = a\left( {x - 5} \right)\left( \ldots \right).\) Điền biểu thức thích hợp vào dấu …
A. 2a + b
B. 1 + b
C. a2 + ab
D. a + b
-
Câu 18:
Phân tích đa thức 3x(x – 3y) + 9y(3y – x) thành nhân tử ta được
A. 3(x – 3y)2
B. (x – 3y)(3x + 9y)
C. (x – 3y) + (3 – 9y)
D. (x – 3y) + (3x – 9y)
-
Câu 19:
Phân tích đa thức \({x^2} - 6x + 8\) thành nhân tử ta được
A. (x – 4)(x – 2)
B. (x – 4)(x + 2)
C. (x + 4)(x – 2)
D. (x – 4)(2 – x)
-
Câu 20:
Giá trị của biểu thức \(A = {x^2} - 4{y^2} + 4x + 4\) tại x = 62, y = -18 là
A. 2800
B. 1400
C. -2800
D. -1400
-
Câu 21:
Cho biểu thức C = xyz – (xy + yz + zx) + x + y + z – 1. Phân tích C thành nhân tử và tính giá trị của C khi x = 9; y = 10; z = 101.
A. C = (z – 1)(xy – y – x + 1); C = 720
B. C = (z – 1)(y – 1)(x + 1); C = 7200
C. C = (z – 1)(y – 1)(x – 1); C = 7200
D. C = (z + 1)(y – 1)(x – 1); C = 7200
-
Câu 22:
Kết quả của phép chia \(15{x^3}{y^4}:5{x^2}{y^2}\) là
A. 3xy2
B. -3x2y
C. 5xy
D. 15xy2
-
Câu 23:
Giá trị số tự nhiên n để phép chia \({x^{2n}}:{x^4}\) thực hiện được là:
A. n \( \in \) N, n > 2
B. n \( \in \) N, n ≥ 4
C. n \( \in \) N, n ≥ 2
D. n \( \in \) N, n ≤ 2
-
Câu 24:
Cho \(A = {\left( {3{a^2}b} \right)^3}{\left( {a{b^3}} \right)^2};B = {\left( {{a^2}b} \right)^4}\). Khi đó A : B bằng
A. 27ab5
B. -27b5
C. 27b5
D. 9b5
-
Câu 25:
Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho DE // BC. Chọn đáp án đúng nhất. Tứ giác BDEC là hình gì?
A. Hình thang
B. Hình thang vuông
C. Hình thang cân
D. Cả A, B, C đều sai
-
Câu 26:
Cho hình thang cân ABCD đáy nhỏ AB = 12cm, đáy lớn CD = 22cm, cạnh bên BC = 13cm thì đường cao AH bằng:
A. 9 cm
B. 8 cm
C. 12 cm
D. 6 cm
-
Câu 27:
Chọn câu đúng nhất.
A. Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
B. Trong hình thang cân, hai cạnh bên bằng nhau.
C. Trong hình thang cân, hai đường chéo bằng nhau.
D. Cả A, B, C đều đúng.
-
Câu 28:
Hãy chọn câu sai.
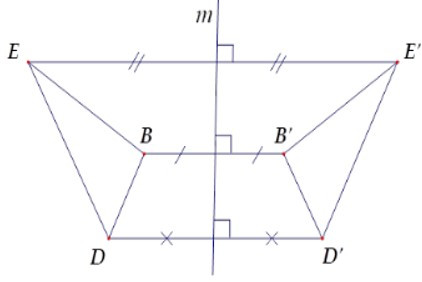
A. Hai đoạn thẳng EB và E’B’ đối xứng nhau qua m.
B. Hai đoạn thẳng DB và D’B’ đối xứng nhau qua m.
C. Hai tam giác DEB và D’E’B’ đối xứng nhau qua m.
D. Hai đoạn thẳng DE và D’B’ đối xứng nhau qua m.
-
Câu 29:
Cho ΔABC và ΔA’B’C’ đối xứng nhau qua đường thẳng d biết AB = 8cm, BC = 11cm và chu vi của tam giác ABC = 30 cm. Khi đó độ dài cạnh C’A’ của tam giác A’B’C’ là:
A. 16cm
B. 15cm
C. 8cm
D. 11cm
-
Câu 30:
Cho tam giác ABC cân tại B, các đường trung tuyến AA’, BB’, CC’. Trục đối xứng của tam giác ABC là:
A. AA’
B. BB’
C. AA’ và CC’
D. CC’
-
Câu 31:
Thương của phép chia \(( - 12{x^4}y + 4{x^3} - 8{x^2}{y^2}):( - 4{x^2})\) bằng:
A. -3x2y + x – 2y2
B. 3x4y + x3 – 2x2y2
C. -12x2y + 4x – 2y2
D. 3x2y – x + 2y2
-
Câu 32:
Cho \(\left( {3x - 4y} \right).\left( \ldots \right) = 27{x^3} - 64{y^3}.\). Điền vào chỗ trống (…) đa thức thích hợp:
A. 6x2 + 12xy + 8y2
B. 9x2 + 12xy + 16y2
C. 9x2 – 12xy + 16y2
D. 3x2 + 12xy + 4y2
-
Câu 33:
Kết quả của phép chia \((2{x^3} - {x^2}\; + 10x):x\) là
A. x2 – x + 10
B. 2x2 – x + 10
C. 2x2 – x – 10
D. 2x2 + x + 10
-
Câu 34:
Cho tứ giác ABCD, lấy M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác ABCD cần có điều kiện gì để MNPQ là hình chữ nhật
A. AB = BC
B. BC = CD
C. AD = CD
D. AC⊥ BD
-
Câu 35:
Chọn câu đúng: Cho tứ giác ABCD có:
A. \(\widehat A = \widehat B = \widehat C = {90^0}\) thì tứ giác ABCD là hình chữ nhật
B. AB = CD; AC = BD thì tứ giác ABCD là hình chữ nhật
C. AB = BC; AD // BC, 900 thì tứ giác ABCD là hình chữ nhật
D. AB // CD; AB = CD thì tứ giác ABCD là hình chữ nhật
-
Câu 36:
Hãy chọn câu đúng. Cho ΔABC với M thuộc cạnh BC. Từ M vẽ ME song song với AB và MF song song với AC. Hãy xác định điều kiện của ΔABC để tứ giác AEMF là hình chữ nhật.
A. ΔABC vuông tại A
B. ΔABC vuông tại B
C. ΔABC vuông tại C
D. ΔABC đều
-
Câu 37:
Phép chia đa thức \((4{x^4} + 3{x^2} - 2x + 1)\) cho đa thức \({x^2} + 1\) được đa thức dư là:
A. 2x + 2
B. -2x + 2
C. -2x - 2
D. 3 - 2x
-
Câu 38:
Kết quả của phép chia \(\left( {2{a^3} + 7a{b^2} - 7{a^2}b - 2{b^3}} \right):\left( {2a - b} \right)\) là:
A. (a – b)(a – 2b)
B. (a + b)2
C. (a – b)(b – 2a)
D. a – b
-
Câu 39:
Hãy chọn câu sai:
A. Tứ giác có hai cặp cạnh đối song song là hình bình hành
B. Hình thang có hai góc kề một đáy bằng nhau là hình bình hành
C. Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành
D. Tứ giác có hai cặp góc đối bằng nhau là hình bình hành
-
Câu 40:
Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở E, F. Chọn khẳng định đúng.
A. DE = FE; FE > FB
B. DE = FE = FB
C. DE > FE; EF = FB
D. DE > FE > FB














