Đề thi giữa HK1 môn Toán 10 năm 2023-2024
Trường THPT Phan Chu Trinh
-
Câu 1:
Mệnh đề nào sau đây là phủ định của mệnh đề: “\(\exists x \in \mathbb{R}|{x^2} - 3x + 2 > 0\)”?
A. \(\exists x \in \mathbb{R}|{x^2} - 3x + 2 < 0\)
B. \(\exists x \in \mathbb{R}|{x^2} - 3x + 2 \le 0\)
C. \(\forall x \in \mathbb{R}|{x^2} - 3x + 2 \le 0\)
D. \(\forall x \in \mathbb{R}|{x^2} - 3x + 2 > 0\)
-
Câu 2:
Cho tập hợp \(A = \{ 1;2;5;7;8\} \) và \(B = \{ x \in \mathbb{N}|x \le 3\} \). Tìm tập hợp \(A \cap B\)?
A. \(\{ 1;2\} \).
B. \(\{ 1\} \).
C. \(\{ 2\} \).
D. \(\emptyset \)
-
Câu 3:
Mỗi học sinh của lớp 10A đều thích môn Toán hoặc môn Tiếng Anh, biết rằng có 30 học sinh thích môn Toán, 25 học sinh thích môn Tiếng Anh và 15 em học sinh thích cả hai môn. Hỏi lớp 10A có tất cả bao nhiêu học sinh?
A. 70
B. 60
C. 50
D. 40
-
Câu 4:
Tính số tập hợp con của tập hợp A có 5 phần tử?
A. \(20\).
B. \(25\).
C. \(32\).
D. \(35\).
-
Câu 5:
Cặp số nào sau đây là nghiệm của bpt: \(3(x - 1) + 4(y - 2) < 5x + 3\)?
A. \((2;5)\).
B. \(( - 2;3)\).
C. \((0;6)\).
D. \((4;5)\).
-
Câu 6:
GTNN của \(F(x;y) = x - 3y\), với điều kiện \(\left\{ \begin{matrix} x\ge 0 \\ 0\le y\le 5 \\ x+y-2\ge 0 \\ 3x-y\le 6 \\ \end{matrix} \right.\)?
A. \(2\)
B. \( - 6\)
C. \( - \frac{{34}}{3}\)
D. \( - 15\)
-
Câu 7:
Cho \(\cos x = \frac{1}{2}\). Tính giá trị của biểu thức \(P = 5{\sin ^2}x + 1\)?
A. \(\frac{{19}}{2}\).
B. \(\frac{{19}}{4}\).
C. \(\frac{{25}}{4}\).
D. \(\frac{3}{4}\).
-
Câu 8:
Cho biết giá trị của \(T = {\cos ^4}x\;(2{\cos ^2}x - 3) + {\sin ^4}x\;(2{\sin ^2}x - 3)\) là?
A. \(1\)
B. \(0\).
C. \( - 1\).
D. \( - 2\).
-
Câu 9:
Nếu tam giác ABC có \(\frac{{\sin B}}{{\sin C}} = 2\cos A\) thì...?
A. Tam giác ABC vuông tại A
B. Tam giác ABC cân tại A
C. Tam giác ABC cân tại B
D. Tam giác ABC cân tại C
-
Câu 10:
Cho tam giác ABC có \(a = 4,b = 5,c = 7\). Bán kính ĐT ngoại tiếp R của tam giác ABC bằng?
A. \(1,02\)
B. \(3,57\)
C. \(14,29\).
D. \(7,62\).
-
Câu 11:
Cho tam giác \(ABC\) có \(c = 32,\widehat A = {70^o},\widehat C = {45^o}\). Tính độ dài cạnh AC?
A. \(39\).
B. \(40\).
C. \(41\).
D. \(42\).
-
Câu 12:
Mệnh đề phủ định của mệnh đề sau “2022 là một số chẵn” là?
A. “-2022 không là một số chẵn”
B. “2022 không là một số chẵn”
C. “-2022 là một số lẻ”
D. “2022 là một số lẻ”
-
Câu 13:
Cho mệnh đề: “Nếu tam giác có hai góc bằng \({60^ \circ }\) thì tam giác đó là tam giác đều”. Mệnh đề đảo của mệnh đề đã cho là?
A. “Nếu tam giác có hai góc bằng \({60^ \circ }\) thì tam giác đó không là tam giác đều”
B. “Nếu tam giác là tam giác đều thì tam giác đó có hai góc bằng \({60^ \circ }\)”
C. “Tam giác là tam giác đều nếu và chỉ nếu tam giác đó có hai góc bằng \({60^ \circ }\)”
D. “Nếu một tam giác là tam giác đều thì tam giác đó có hai góc bằng nhau”
-
Câu 14:
Viết mệnh đề sau bằng kí hiệu \(\forall \) hoặc \(\exists \): “Có một số nguyên bằng bình phương của chính nó”?
A. \(\exists \;x \in \mathbb{R},{x^2} - x = 0\)
B. \(\exists \;x \in \mathbb{R},x = {x^2}\)
C. \(\forall \;x \in \mathbb{Z},{x^2} = x\)
D. \(\exists \;x \in \mathbb{Z},x = {x^2}\)
-
Câu 15:
Hãy viết tập hợp \(A = \{ - 4; - 3; - 2; - 1;0;1;2;3;4\} \) bằng cách chỉ ra tính chất đặc trưng?
A. \(A = \{ x \in \mathbb{R}|\left| x \right| < 4\} \)
B. \(A = \{ x \in \mathbb{Z}|\left| x \right| < 4\} \)
C. \(A = \{ x \in \mathbb{R}|\left| x \right| \le 4\} \)
D. \(A = \{ x \in \mathbb{Z}|\left| x \right| \le 4\} \)
-
Câu 16:
Dùng kí hiệu khoảng, đoạn, nửa khoảng để viết lại tập hợp \(A = \{ x \in \mathbb{R}| - 5 \le x < 3\} \)?
A. \(( - 5;3)\)
B. \(( - 5;3]\)
C. \([ - 5;3]\)
D. \([ - 5;3)\)
-
Câu 17:
Kết quả của \(( - 1;4] \cap ( - \infty ;3)\) bằng bao nhiêu?
A. \(( - 1;3)\)
B. \([3;4]\)
C. \(( - \infty ;4]\)
D. \(( - \infty ; - 1]\)
-
Câu 18:
Tìm phần bù của \([ - 1;5)\) trong \(\mathbb{R}\)?
A. \(( - \infty ; - 1]\)
B. \(( - \infty ; - 1) \cup [5; + \infty )\)
C. \(( - \infty ; - 1)\)
D. \((5; + \infty )\)
-
Câu 19:
Bất phương trình nào là bất phương trình bậc nhất hai ẩn?
A. \(2{x^2} - 3y < 0\)
B. \( - x + 4y > - 3\)
C. \(x + {y^2} \ge 2\)
D. \({x^2} + 4{y^2} \le 6\)
-
Câu 20:
Hình vẽ sau là biểu diễn của tập hợp nào?
A. \(( - \infty ; - 2) \cup [5; + \infty )\)
B. \(( - \infty ; - 2) \cup (5; + \infty )\)
C. \(( - \infty ; - 2] \cup (5; + \infty )\)
D. \(( - \infty ; - 2] \cup [5; + \infty )\)
-
Câu 21:
Biết \({C_\mathbb{R}}A = [ - 3;11)\) và \({C_\mathbb{R}}B = ( - 8;1]\). Khi đó \({C_\mathbb{R}}\left( {A \cap B} \right)\) bằng?
A. \([ - 3;1]\)
B. \(( - \infty ; - 8] \cup [11; + \infty )\)
C. \(( - 8;11)\)
D. \(( - \infty ; - 3) \cup (1; + \infty )\)
-
Câu 22:
Miền không tô màu dưới đây biểu diễn miền nghiệm của bpt nào?
A. \(x + 2y \le 1\)
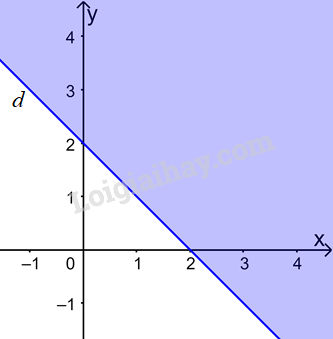
B. \(x + 2y \ge 1\)
C. \(x + y \ge 2\)
D. \(x + y \le 2\)
-
Câu 23:
Miền tam giác ABC kể cả 3 cạnh AB, BC, CA trong hình là miền nghiệm của hệ bpt nào trong 4 hệ bất phương trình sau đây?
A. \(\left\{ \begin{array}{l}x + y - 2 \le 0\\x - y + 2 \ge 0\\x - 2y + 2 \le 0\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x + y - 2 \ge 0\\x - y + 2 \ge 0\\x - 2y + 2 \le 0\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x + y - 2 \le 0\\x - y + 2 \le 0\\x - 2y + 2 \le 0\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x + y - 2 \le 0\\x - y + 2 \ge 0\\x - 2y + 2 \ge 0\end{array} \right.\)
-
Câu 24:
Chọn khẳng định sai trong các khẳng định dưới?
A. \(\cot ({180^ \circ } - \alpha ) = - \cot \alpha \)
B. \(\cos ({180^ \circ } - \alpha ) = \cos \alpha \)
C. \(\tan ({180^ \circ } - \alpha ) = \tan \alpha \)
D. \(\sin ({180^ \circ } - \alpha ) = - \sin \alpha \)
-
Câu 25:
Tam giác ABC có \(a = 8,b = 3,B = {60^ \circ }\). Tính độ dài của cạnh \(b\)?
A. \(49\)
B. \(\sqrt {97} \)
C. \(7\)
D. \(\sqrt {61} \)
-
Câu 26:
Cho tam giác ABC có \(B = {30^ \circ },C = {45^ \circ },AB = 3\). Tính cạnh AC?
A. \(\frac{{3\sqrt 6 }}{2}\)
B. \(\frac{{3\sqrt 2 }}{2}\)
C. \(\sqrt 6 \)
D. \(\frac{{2\sqrt 6 }}{3}\)
-
Câu 27:
Tam giác ABC cân tại A có \(A = {120^ \circ }\). Trong các khẳng định sau, khẳng định đúng là?
A. \(BC = 2AB\)
B. \(BC = 2\sqrt 5 AB\)
C. \(BC = AB\sqrt 5 \)
D. \(BC = AB\sqrt 3 \)
-
Câu 28:
Tam giác ABC có góc A nhọn, AB = 5, AC = 8 và S bằng 12. Tính độ dài cạnh BC?
A. \(2\sqrt 3 \)
B. \(4\)
C. \(3\sqrt 2 \)
D. \(5\)
-
Câu 29:
Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc \({60^ \circ }\). Biết \(CA = 200(m),CB = 180(m)\). Khoảng cách AB là?
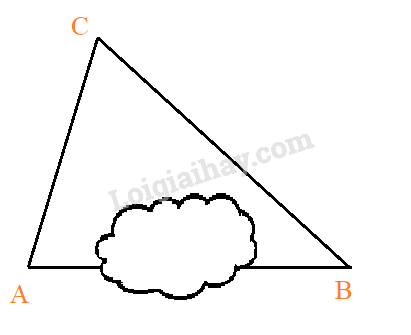
A. \(168\sqrt 7 (m)\)
B. \(228(m)\)
C. \(20\sqrt {91} (m)\)
D. \(112\sqrt {17} (m)\)
-
Câu 30:
Kí hiệu nào viết đúng về mệnh đề: “\(\sqrt 5 \) không là số nguyên”?
A. \(\sqrt 5 = \mathbb{Z}\)
B. \(\sqrt 5 \in \mathbb{Z}\)
C. \(\sqrt 5 \subset \mathbb{Z}\)
D. \(\sqrt 5 \notin \mathbb{Z}\)
-
Câu 31:
Trong các mệnh đề sau, mệnh đề nào là đúng?
A. \(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > - 1\).
B. \(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > 1\).
C. \(\forall x \in \mathbb{R},x > - 1 \Rightarrow {x^2} > 1\).
D. \(\forall x \in \mathbb{R},x > 1 \Rightarrow {x^2} > 1\)
-
Câu 32:
Cho \(A = \{ n = 2k|k \in \mathbb{N},k \le 3\} \) , \(B = \{ n \in \mathbb{N}|n \le 5\} \) và \(C = \{ n \in \mathbb{N}|2 \le n \le 6\} \). Tìm tập hợp sau: \(A{\rm{\backslash }}\left( {B \cup C} \right)\)?
A. \(\{ 0;8\} \)
B. \(\{ 0\} \).
C. \(\{ 8\} \).
D. \(\emptyset \).
-
Câu 33:
Cho \(A = ( - 2;5]\) và \(B = (m; + \infty )\). Tìm \(m \in \mathbb{Z}\) để \(A{\rm{\backslash }}B\) chứa đúng 5 số nguyên?
A. 1
B. 3
C. 5
D. 7
-
Câu 34:
Lớp 10A có 45 học sinh trong đó có 23 em thích môn Văn, 20 em thích môn Toán, 12 em không thích môn nào. Số em thích cả hai môn trên là?
A. 8
B. 10
C. 12
D. 14
-
Câu 35:
GTLN của \(F(x;y) = 5x - 3y\), với đk \(\left\{ \begin{array}{*{35}{l}} x\ge 0 \\ 0\le y\le 5 \\ x+y-2\ge 0 \\ 3x-y\le 6 \\ \end{array} \right.\text{ }\)?
A. \( - 2\)
B. \(10\)
C. \(\frac{{10}}{3}\)
D. \( - 15\)
-
Câu 36:
Cho góc \(x\;({0^ \circ } < x < {180^ \circ })\) thỏa mãn \(\tan x = 5\). Tính biểu thức: \(P = \frac{{3\sin x + 11\cos x}}{{7\sin x - 9\cos x}}\)?
A. \(\frac{{ - 29}}{{19}}\).
B. \(\frac{{29}}{{19}}\).
C. \( - 1\).
D. \(1\).
-
Câu 37:
Rút gọn biểu thức sau: \(A = \frac{{\sin x + \sin 3x + \sin 5x}}{{\cos x + \cos 3x + \cos 5x}}\)?
A. \(\sin 3x\)
B. \(\cos 3x\).
C. \(\tan 3x\).
D. \(\tan x\).
-
Câu 38:
Cho tam giác ABC. Mệnh đề nào đúng?
A. \(\sin (A + B) = - \sin C\)
B. \(\sin \left( {\frac{{A + B}}{2}} \right) = \cos \frac{C}{2}\)
C. \(\cos (A + B) = \cos C\)
D. \(\tan (A + B) = \tan C\)
-
Câu 39:
Cho tam giác ABC có \(BC = 5,\widehat {BAC} = {120^o}\). Bán kính ĐT ngoại tiếp \(\Delta ABC\) bằng?
A. \(R = \frac{{5\sqrt 3 }}{2}\)
B. \(R = \frac{5}{2}\)
C. \(R = \frac{{5\sqrt 3 }}{3}\)
D. \(R = 5\)
-
Câu 40:
Cho tam giác \(ABC\) có \(c = 4,b = 7,\widehat A = {60^ \circ }\). Tính chiều cao \({h_a}\) của tam giác ABC (làm tròn đến hàng đơn vị)?
A. 3
B. 2
C. 4
D. 5
