Tại hai đỉnh A, B của một tam giác đều ABC cạnh a đặt hai điện tích điểm \( q_1=q_2=4.10^{−9}C\) trong không khí. Hỏi phải đặt điện tích q3 có giá trị bao nhiêu tại C để cường độ điện trường gây ra bởi hệ ba điện tích tại trọng tâm G của tam giác bằng 0.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
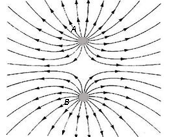
Báo sai
+ Các điện tích tại các đỉnh A, B, C của tam giác ABC gây ra tại trọng tâm G của tam giác các véctơ cường độ điện trường \( \overrightarrow {{E_A}} ; \overrightarrow {{E_B}} ; \overrightarrow {{E_C}} \) có phương chiều như hình vẽ và độ lớn.
\(\left\{ \begin{array}{l} {E_A} = {E_B} = \frac{{k{q_1}}}{{{{\left( {\frac{2}{3}\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = \frac{{3k{q_1}}}{{{a^2}}}\\ {E_C} = \frac{{k{q_3}}}{{{{\left( {\frac{2}{3}\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = \frac{{3k{q_3}}}{{{a^2}}} \end{array} \right.\)
Cường độ điện trường tổng hợp tại G:
\( \overrightarrow E = \overrightarrow {{E_A}} + \overrightarrow {{E_B}} + \overrightarrow {{E_C}} \)
+ Vì các véctơ cường độ điện trường lần lượt hợp nhau một góc 120º và \(E_A=E_B\) nên để E = 0 thì \(q_1=q_2=q_3=4.10^{-9}C\)
Câu hỏi liên quan
-
Một điện tích điểm q = 106 C đặt trong không khí. Xác định cường độ điện trường tại điểm cách điện tích 30cm
-
Nếu khoảng cách từ điện tích nguồn tới điểm đang xét tăng 2 lần thì cường độ điện trường
-
Cho 2 điện tích điểm trái dấu, cùng độ lớn nằm cố định thì
-
Độ lớn cường độ điện trường tại một điểm gây bởi một điện tích điểm không phụ thuộc
-
Phát biểu nào sau đây là không đúng?
-
Một electron bay trong điện trường đều giữa hai bản kim loại phẳng tích điện trái dấu từ bản âm sang bản dương. Khoảng cách giữa hai bản là 2cm.Cường độ điện trường đều là 9.104V/m. Electron có điện tích e=1,6.10−19C. khối lượng m=9,1.10−31kg, vận tốc ban đầu của electron bằng 0.Thời gian bay của electron là:
-
Vectơ cường độ điện trường tại một điểm trong điện trường luôn:
-
Khái niệm nào sau đây cho biết độ mạnh yếu của điện trường tại một điểm?
-
Trong mỗi giây có 109 hạt electron đi qua tiết diện thẳng của một ống phóng điện. Biết điện tích mỗi hạt có độ lớn bằng 1,6.10−19C. Tính cường độ dòng điện qua ống?
-
Nếu tại một điểm có 2 điện trường gây bởi 2 điện tích điểm Q1 âm và Q2 dương thì hướng của cường độ điện trường tại điểm đó được xác định bằng
-
Cường độ điện trường là đại lượng
-
Điện trường là
-
Cường độ điện trường của một điện tích phụ thuộc vào khoảng cách r được mô tả như đồ thị bên. Biết r2 = r1 + r32 và các điểm cùng nằm trên một đường sức. Giá trị của x bằng
.png)
-
Một điện tích điểm q đặt trong môi trường đồng tính có hằng số điện môi 2,5. Tại điểm M cách q một đoạn 4cm vec tơ cường độ điện trường do điện tích đó gây ra có độ lớn 9.105V/m và hướng về phía q. Ta có:
-
Một quả cầu nhỏ khối lượng 2√3g mang điện tích 10−5C được treo ở đầu một sợi chỉ tơ đặt trong điện trường đều có vecto cường độ điện trường \( \overrightarrow E \) nằm ngang (E = 2000 V/m). Khi quả cầu nằm cân bằng, dây treo lệch với phương thẳng đứng góc α là
-
Đặt bốn điện tích có cùng độ lớn q tại bốn đỉnh của một hình vuông ABCD cạnh a với điện tích dương đặt tại A, D, điện tích âm đặt tại B và C. Xác định cường độ điện trường tổng hợp tại giao điểm hai đường chéo của hình vuông.
-
Chọn phát biểu sai:
-
Tính cường độ điện trường do một điện tích điểm +4.10−9C gây ra tại một điểm cách nó 5cm trong chân không
-
Công thức xác định cường độ điện trường gây ra bởi điện tích Q < 0, tại một điểm trong chân không, cách điện tích Q một khoảng r là
-
Phát biểu nào sau đây là sai khi nói về đường sức của điện trường.
