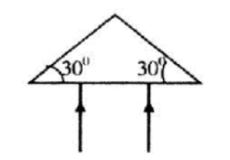
Một lăng kính thủy tinh có chiết suất \(n=\sqrt{2},\) góc chiết quang \(A={{60}^{0}}.\) Tia SI từ đáy truyền lên tới lăng kính với góc tới \({{i}_{1}}.\) Để không có tia ló ra ở mặt bên thứ hai thì góc tới \({{i}_{1}}.\) phải thỏa
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiLăng kính thủy tinh có góc chiết quang \(A={{60}^{0}}\) thì có tiết diện là tam giác đều.
Để không có tia ló tại mặt bên kia thì
\({{r}_{2}}\ge {{i}_{gh}}\Rightarrow \sin {{r}_{2}}\ge \frac{1}{n}\Rightarrow \sin {{r}_{2}}\ge \frac{1}{\sqrt{2}}\Rightarrow {{r}_{2}}\ge \arcsin \left( \frac{\sqrt{2}}{2} \right)={{45}^{0}}.\)
Ta có: \(A={{r}_{1}}+{{r}_{2}}\Rightarrow {{r}_{1}}=A-{{r}_{2}}.\)
Mà \({{r}_{2}}\ge {{45}^{0}}\Rightarrow {{r}_{1}}\le A-{{r}_{2}}\Rightarrow {{r}_{1}}\le 15{}^{0}.\)
Định luật khúc xạ ánh sáng tại I:
\(\sin {{i}_{1}}=n\sin {{r}_{1}}\le \sqrt{2}.\sin {{15}^{0}}.\)
\(\Leftrightarrow \sin {{i}_{1}}\le \sqrt{2}.\sin {{15}^{0}}.\)
\(\Rightarrow {{i}_{1}}\le {{21}^{0}}28'.\)
Câu hỏi liên quan
-
Một lăng kính thủy tinh có chiết xuất n = 1,5. Chiếu một tia sáng qua lăng kính, để góc lệch cực tiểu bằng góc chiết quang A thì góc chiết quang A phải bằng
-
Phát biểu nào sau đây là không đúng? Chiếu một chùm sáng vào mặt bên của một lăng kính đặt trong không khí:
-
Chọn câu sai. Chiếu một chùm tia sáng vào một mặt bên của lăng kính ở trong không khí thì
-
Một lăng kính thủy tinh có chiết suất n=√2 . Tiết diện thẳng của lăng kính là một tam giác đều ABC. Chiếu một tia sáng nằm trong mặt phẳng của tiết diện thẳng, tới AB với góc tới i1=450 . Góc lệch D của lăng kính có giá trị là:
-
Lăng kính phản xạ toàn phần là một khối lăng trụ thủy tinh có tiết diện thẳng là:
-
Chọn câu trả lời đúng. Hai tia sáng song song chiếu thẳng góc vào mặt đáy của lăng kính như hình vẽ , có chiết suất n=√2. Góc giữa hai tia ló là:
-
Hình vẽ bên là đường truyền của tia sáng đơn sắc qua lăng kính đặt trong không khí có chiết suất n=√2 . Biết tia tới vuông góc với mặt bên AB và tia ló ra khỏi lăng kính đi là là mặt AC. Tính góc chiết quang A của lăng kính?
.PNG)
-
Biết một lăng kính có tiết diện thẳng là tam giác ABC, góc chiết quang A. tia sáng đi tới mặt bên AB và ló ra mặt bên AC. So với tia tới thì tia ló
-
Một lăng kính thủy tinh có chiết suất n=1,6. Chiếu một tia sáng đơn sắc theo phương vuông góc với mặt bên của lăng kính. Tia sáng phản xạ toàn phần ở mặt bên của lăng kính. Tính giá trị nhỏ nhất của góc chiết quang A.
-
Công thức định góc lệch của tia sáng đơn sắc qua lăng kính là
-
Một lăng kính có chiết suất n = 1,5 góc chiết quang nhỏ \(A={{6}^{0}}.\) Chiếu tia sáng vào mặt bên dưới góc tới nhỏ. Góc lệch của tia ló qua lăng kính có trị số
-
Một lăng kính có tiết diện thẳng là tam giác đều, ba mặt như nhau, chiết suất n=√3 , được đặt trong không khí. Chiếu tia sáng đơn sắc nằm trong mặt phẳng tiết diện thẳng, vào mặt bên của lăng kính với góc tới i=600 . Góc lệch D của tia ló và tia tới bằng:
-
Tiêu cự của thấu kính được tính bởi công thức
-
Chiếu một chùm tia sáng song song tới lăng kính. Cho i tăng dần từ giá trị nhỏ nhất thì góc lệch D sẽ
-
Lăng kính thủy tinh có n = 1,5; góc chiết quang \(A={{60}^{0}}.\) Chiếu một chùm tia sáng hẹp đơn sắc tới lăng kính trong mặt phẳng của tiết diện vuông góc. Nếu tia ló và tia tới đối xứng nhau qua mặt phẳng phân giác của A thì góc lệch sẽ là
-
Lăng kính có góc chiết quang A = 600, chiết suất \(n=\sqrt{2}.\) Góc lệch D đạt giá trị cực tiểu khi góc tới i có giá trị
-
Một lăng kính có chiết suất n, góc chiết quang \(A={{60}^{0}}.\) Một chùm tia sáng đơn sắc được chiếu tới mặt bên AB cho chùm tia ló ở mặt sau AC của lăng kính. Điều chỉnh tia tới để có góc lệch cực tiểu, người ta đo được góc lệch Dmin = 600. Chiết suất n của lăng kính là
-
Tia tới vuông góc với mặt bên của lăng kính thuỷ tinh có chiết suất n = 1,5 góc chiết quang A. Tia ló hợp với tia tới một góc lệch D = 300. Góc chiết quang của lăng kính là
-
Lăng kính phản xạ toàn phần có tiết diện là
-
Sử dụng hình vẽ về đường đi của tia sáng qua lăng kính: SI là tia tới, JR là tia ló, D là góc lệch giữa tia tới và tia ló, n là chiết suất của chất làm lăng kính. Công thức nào trong các công thức sau đây là đúng?
