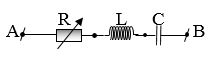
Một đoạn mạch xoay chiều gồm điện trở thuần R = 100 Ω, một cuộn dây thuần cảm có độ tự cảm \(L=\frac{2}{\pi }\text{ }H\) và một tụ điện có điện dung \(C=\frac{{{10}^{-4}}}{\pi }\text{ }F\) mắc nối tiếp giữa hai điểm có điện áp \(u=200\sqrt{2}\cos \left( 100\pi t \right)\text{ }(V).\) Điện áp hai đầu cuộn cảm là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiCảm kháng và dung kháng của mạch: \({{Z}_{L}}=\omega L=200\text{ }\Omega ;\text{ }{{Z}_{C}}=\frac{1}{\omega C}=100\text{ }\Omega .\)
Độ lệch pha giữa điện áp hai đầu đoạn mạch và cường độ dòng điện:
\(\tan \left( {{\varphi }_{u}}-{{\varphi }_{i}} \right)=\frac{{{Z}_{L}}-{{Z}_{C}}}{R}=1\Rightarrow {{\varphi }_{u}}-{{\varphi }_{i}}=\frac{\pi }{4}.\)
Độ lệch pha giữa điện áp hai đầu đoạn mạch và điện áp hai đầu cuộn dây:
\({{\varphi }_{L}}-{{\varphi }_{u}}=\left( {{\varphi }_{L}}-{{\varphi }_{i}} \right)-\left( {{\varphi }_{u}}-{{\varphi }_{i}} \right)=\frac{\pi }{2}-\frac{\pi }{4}=\frac{\pi }{4}\Rightarrow {{\varphi }_{L}}=\frac{\pi }{4}+{{\varphi }_{u}}=\frac{\pi }{4}.\)
Ta có: \(\frac{{{U}_{0L}}}{{{U}_{0}}}=\frac{{{Z}_{L}}}{Z}=\frac{{{Z}_{L}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}=\sqrt{2}\Rightarrow {{U}_{0L}}={{U}_{0}}\sqrt{2}=400\text{ V}\text{.}\)
Biểu thức điện áp hai đầu cuộn dây: \({{u}_{L}}=400\text{cos}\left( 100\pi t+\frac{\pi }{4} \right)\text{ }(V).\)
Câu hỏi liên quan
-
Đặt vào 2 đầu một hộp kín X gồm các phần tử mắc nối tiếp (các phần tử có thể là điện trở R, tụ điện có điện dung C và cuộn cảm thuần có độ tự cảm L) một điện áp\(u=50cos\left( 100\pi t+\frac{\pi }{6} \right)\text{ }(\text{V})\) thì cường độ dòng điện qua mạch là \(i=2cos\left( 100\pi t+\frac{2\pi }{3} \right)\text{ }(A).\) Nếu thay điện áp trên bằng điện áp khác có biểu thức \(u=50\sqrt{2}cos\left( 200\pi t+\frac{2\pi }{3} \right)\text{ }(\text{V})\) thì cường độ dòng điện sẽ là \(i=\sqrt{2}cos\left( 200\pi t+\frac{\pi }{6} \right)\text{ }(A).\) Hộp kín X chứa
-
Trong một đoạn mạch xoay chiều không phân nhánh, cường độ dòng điện sớm pha một góc φ so với điện áp ở hai đầu đoạn mạch \(\left( 0<\varphi <\frac{\pi }{2} \right).\) Đoạn mạch đó:
-
Đoạn mạch điện xoay chiều không phân nhánh gồm cuộn dây có độ tự cảm L, điện trở thuần R và tụ điện có điện dung C. Khi dòng điện có tần số góc \(\frac{1}{{\sqrt {LC} }}\) chạy qua đoạn mạch thì hệ số công suất của đoạn mạch này
-
Mắc mạch điện xoay chiều R, L, C nối tiếp vào điện áp \(u=U_0cos(100\pi t+ \frac{\pi }{2})\) thì dòng điện qua mạch là \(i=I_0cos(100\pi t+ \frac{\pi }{6})\). Kết luận nào sau đây đúng:
-
Cho một đoạn mạch điện xoay chiều gồm điện trở thuần R và một cuộn cảm thuần có hệ số tự cảm L. Điện áp hai đầu đoạn mạch có biểu thức \(u=100\sqrt{2}\cos \left( 100\pi t+\varphi \right)\text{ }(V).\)Cường độ dòng điện trong mạch có giá trị hiệu dụng là 2 A và chậm pha hơn điện áp góc \(\frac{\pi }{3}.\) Giá trị của điện trở thuần R là:
A. B. $$ C. D. $$
-
Cho mạch điện xoay chiều không phân nhánh RLC. Đặt vào hai đầu mạch điện một điện áp xoay chiều có biểu thức \(u={{U}_{0}}\text{sin }\!\!\omega\!\!\text{ t (V)}.\) Điều kiện để có cộng hưởng điện trong mạch là
-
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gốm điện trở R mắc nối tiếp với cuộn cảm thuần thì cảm kháng và tổng trở của đoạn mạch lần lượt là ZL và Z. Hệ số công suất của đoạn mạch là cosφ. Công thức nào sau đây đúng?
-
Mạch R, L, C mắc nối tiếp có hệ số công suất bằng 1 khi
-
Mạch RLC có R thay đổi được được mắc vào mạng điện xoay chiều có tần số không thay đổi, R bằng bao nhiêu thì mạch đạt công suất cực đại? (Không có hiện tượng cộng hưởng xảy ra).
-
Đặt điện áp u = U0coswt (U0 không đổi, w thay đổi được) vào hai đầu đoạn mạch gồm điện trở R, cuộn cảm thuần L và tụ điện C mắc nối tiếp. Hiện tượng cộng hưởng điện xảy ra khi
-
Cho đoạn mạch xoay chiều không phân nhánh gồm cuộn dây thuần cảm có hệ số tự cảm \(L=\frac{2}{\pi }\text{ }H,\) tụ điện \(C=\frac{{{10}^{-4}}}{\pi }\text{ }F\) và một điện trở thuần R. Điện áp đặt vào hai đầu đoạn mạch và cường độ dòng điện qua đoạn mạch có biểu thức là \(u={{U}_{0}}cos(100\pi t)\text{ }V\) và \(i={{I}_{0}}cos\left( 100\pi t-\frac{\pi }{4} \right)A.\) Điện trở R có giá trị là
-
Hiệu điện thế xoay chiều giữa hai đầu một đoạn mạch trễ pha so với cường độ dòng điện trong trường hợp mạch
-
Phát biểu nào sau đày là không đúng? Trong mạch điện xoay chiều không phân nhánh khi điện dung của tụ điện thay đổi và thoả mãn điều kiện \(\omega =\frac{1}{\sqrt{LC}}\) thì
-
Một đoạn mạch xoay chiều gồm cuộn dây mắc nối tiếp với tụ điện. Độ lệch pha giữa cường độ dòng điện trong mạch và điện áp hai đầu mạch là π/3. Điện áp hiệu dụng giữa hai đầu tụ bằng \(\sqrt3 \)lần điện áp hai đầu cuộn dây. Độ lệch pha của điện áp giữa hai đầu cuộn dây so với cường độ dòng điện trong mạch là
-
Trong mạch điện xoay chiều không phân nhánh RLC thì dòng điện nhanh hay chậm pha so với điện áp của đoạn mạch phụ thuộc vào
-
Cho đoạn mạch xoay chiều như hình vẽ: Biết \( L = \frac{1}{\pi }(H);C = \frac{{{{10}^{ - 3}}}}{{4\pi }}F\). Đặt vào hai đầu đoạn mạch một hiệu điện thế :\({U_{AB}} = 75\sqrt 2 \cos (100\pi t)(V)\) Công suất trên toàn mạch là P=45(W). Tính giá trị R?
-
Một đoạn mạch gồm cuộn dây thuần cảm (cảm thuần) mắc nối tiếp với điện trở thuần. Nếu đặt hiệu điện thế \(u=15\sqrt{2}\sin \left( 100\pi t \right)\text{ }(V)\) vào hai đầu đoạn mạch thì hiệu điện thế hiệu dụng giữa hai đầu cuộn dây là 5 V. Khi đó, hiệu điện thế hiệu dụng giữa hai đầu điện trở bằng
-
Nếu dòng xoay chiều chạy qua một cuộn dây chậm pha hơn điện áp hai đầu của nó một góc \(\frac{\pi }{4}\) thì chứng tỏ cuộn dây
-
Đặt một điện áp xoay chiều vào hai đầu đoạn mạch gồm một điện trở thuần R, một cuộn thuần cảm và một tụ điện ghép nối tiếp. Biết R = ZL = 2ZC. Tại thời điểm điện áp tức thời hai đầu cuộn cảm và hai đầu điện trở bằng nhau và bằng 40 V thì điện áp tức thời hai đầu đoạn mạch lúc đó và điện áp cực đại giữa hai đầu mạch là
A. B.
C. D.
-
Đặt điện áp \(\text{u}=1\text{20cos}\left( \text{100}\pi \text{t} \right)\text{ }\left( V \right)\) vào hai đầu một cuộn dây thì dòng điện qua cuộn dây có biểu thức \(i=\text{2cos}\left( \text{100 }\!\!\pi\!\!\text{ t}-\frac{\pi }{6} \right)\text{ }\left( A \right).\) Cảm kháng của cuộn dây là
