ADMICRO
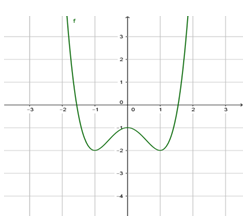
Điểm cực tiểu của đồ thị hàm số y=−x4+2x2+2 là:
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Môn: Toán Lớp 12
Bài: Cực trị của hàm số
ZUNIA12
Lời giải:
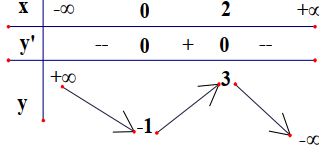
Báo saiy=−x4+2x2+2y′=−4x3+4xy′=0⇔−4x3+4x=0⇔[x=0x=−1x=1y″=−12x2+4y″(0)=4>0⇒x=0 là điểm cực tiểu của hàm số ;yCT=y(0)=2y″(±1)=−8<0⇒x=1 và x=−1 là hai điểm cực đại của hàm số, yCĐ=y(±1)=3
Điểm cực tiểu của đồ thị hàm số là (0;2)
ZUNIA9
AANETWORK



.png)
.png)