ADMICRO
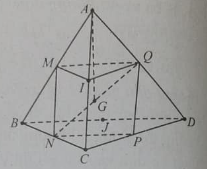
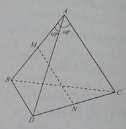
Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Đặt . Khẳng
định nào sau đây đúng?
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ZUNIA12
Lời giải:
Báo sai
ZUNIA9
AANETWORK



.png)