Cho mạch điện như hình vẽ. Cho biết hiệu điện thế U = 24V.
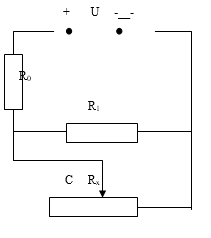
Các điện trở R0 = 6 Ω, R1 = 18 Ω, Rx là một biến trở, dây nối có điện trở không đáng kể. Tính Rx sao cho công suất tiêu hao trên Rx bằng 13,5W và tính hiệu suất của mạch điện. Biết rằng năng lượng điện tiêu hao trên R1 và Rx là có ích, trên R0 là vô ích.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐiện trở tương đương của R1 và Rx:
\({R_{1x}} = \frac{{{\rm{ }}{R_1}{R_x}}}{{{R_1} + {R_x}}} = \frac{{18{R_x}}}{{18 + {R_x}}}\)
Điện trở toàn mạch:
\(R{\rm{ }} = {\rm{ }}{R_0}\; + {\rm{ }}{R_{1x}} = 6 + \frac{{18{R_x}}}{{18 + {R_x}}} = \frac{{24(4,5 + {R_x})}}{{18 + {R_x}}}\)
Cường độ dòng điện qua mạch chính:
\(I = \frac{U}{R} = \frac{{18 + {R_x}}}{{4,5 + {R_x}}}\)
Ta có:
\(\begin{array}{l} {I_x}.{R_x}\; = {\rm{ }}I.{R_{1x}}\\ \Rightarrow {I_x} = \frac{{I.{R_{1x}}}}{{{R_x}}} = \frac{{18}}{{4,5 + {R_x}}} \end{array}\)
Công suất hao phí trên Rx:
\({P_x}\; = {\rm{ }}{I^2}.{R_x} = {\left( {\frac{{18}}{{4,5 + {R_x}}}} \right)^2}{R_x} = 13,5\)
Ta có phương trình bậc 2: \({R_x}^2\; - {\rm{ }}15{R_x}\; + {\rm{ }}20,25{\rm{ }} = {\rm{ }}0\)
Giải phương trình bậc 2 ta được 2 nghiệm Rx = 13,5 Ω và Rx = 1,5 Ω.
Hiệu suất của mạch điện: \(H = \frac{{{P_i}}}{{{P_t}}} = \frac{{{I^2}.{R_{1x}}}}{{{I^2}.R}} = \frac{{{R_{1x}}}}{R}\)
+ Với Rx = 13,5 Ω ta có: \(H = \frac{{18{R_x}}}{{2,5(4,5 + {R_x})}} = 56,25\% \)
+ Với Rx = 1,5 Ω ta có:
\(H = \frac{{18{R_x}}}{{2,5(4,5 + {R_x})}} = 18,75\% \)
Câu hỏi liên quan
-
Với cùng một công suất điện được truyền tải đi trên cùng một đường dây tải điện. Nếu hiệu điện thế ở hai đầu đường dây tăng 4 lần thì:
-
Cho mạch điện (như hình vẽ):
.png)
AB làm biến trở con chạy C có điện trở toàn phần là 120Ω. Nhờ có biến trở làm thay đổi cường độ dòng điện trong mạch từ 0.9A đến 4.5A. Tính công suất toả nhiệt lớn nhất trên biến trở. Biết U không đổi.
-
Dây điện trở của một bếp làm bằng nicrom có điện trở suất 1,1.10-6 Ω.m, chiều dài 3m, tiết diện 0,05 mm2. Bếp sử dụng ở hiệu điện thế U = 220V. Hãy tính công suất của bếp điện, từ đó suy ra nhiệt lượng tỏa ra của bếp trong 30 phút.
-
Một bóng đèn dây tóc có ghi 220V - 60W. Nếu lấy đèn nói trên cắm vào ổ điện U = 110 V (cho rằng điện trở của dây tóc bong đèn không phụ thuộc vào nhiệt độ). Công suất của đèn trong trường hợp này là
-
Muốn nâng 1 vật có trọng lượng 2000N lên cao 10m trong thời gian 50s.Phải dùng động cơ điện nào dưới đây là thích hợp nhất :
-
Một ấm điện khi hoạt động bình thường có điện trở R = 220 Ω và cường độ dòng điện qua bếp là 2A. Tính nhiệt lượng mà bếp tỏa ra trong một phút.
-
Một bóng đèn có điện trở 6\(\Omega\) mắc nối tiếp với điện trở R' vào hiệu điện thế 12V thì bóng đèn sáng bình thường và dòng điện qua điện trở R' là 1,5A. Thông tin nào sau đây là sai?
-
Một bếp điện hoạt động ở hiệu điện thế 220V. Tính nhiệt lượng tỏa ra ở dây dẫn của bếp trong thời gian 25 phút theo đơn vị calo. Biết điện trở của nó là 50Ω.
-
Từ công thức tính công suất hao phí, đề giảm hao phí khi truyền tải điện năng đi xa, ta chọn phương án nào trong các phương án sau:
-
Một ấm điện khi hoạt động bình thường có điện trở R = 220 Ω và cường độ dòng điện qua bếp là 2A. Tính nhiệt lượng mà bếp tỏa ra trong một phút.
-
Hai bóng đèn, một cái có công suất 75W, cái kia có công suất 40W, họat động bình thường dưới hiệu điện thế 120V. Khi so sánh điện trở dây tóc của hai bóng đèn thì
-
Trong công thức P = I2.R Nếu tăng gấp đôi điện trở R và giảm cường độ dòng điện 4 lần thì công suất:
-
Cho mạch điện như hình vẽ (Hình 3). UAB = 90V; R1 = 40 Ω; R2 = 90Ω; R4 = 20Ω; R3 là một biến trở. Bỏ qua điện trở của ampe kế, dây nối và khoá K.
.png)
Khi mở khóa K và điều chỉnh cho R3 = 30Ω. Tính số chỉ của ampe kế.
-
Bóng đèn có điện trở 9 Ω và hiệu điện thế qua nó là 24V thì nó sáng bình thường. Tính công suất định mức của bóng đèn?
-
Trên nhiều dụng cụ trong gia đình thường có ghi 220V và số Woát (W). Số Woát này có ý nghĩa gì?
-
Phát biểu nào sau đây là đúng?
-
Có hai điện trở R1 và R2 = 2R1 được mắc song song vào một hiệu điện thế không đổi. Công suất điện P1 P2 tương ứng trên hai điện trở này có mối quan hệ nào dưới đây?
-
Cho sơ đồ như hình vẽ. R = 4 Ω; R1 là đèn 6V – 3W; R2 là biến trở; UMN không đổi bằng 10V. Xác định R2 để công suất tiêu thụ của mạch song song cực đại.
.png)
-
Trên một bóng đèn có ghi 220V - 100W. Khi bóng đèn sáng bình thường thông tin nào sau đây là sai?
-
Trên hai bóng đèn có ghi (220V - 60W ) và (220V - 75W ). Biết rằng dây tóc của hai bóng đèn này đều bằng vônfram và có tiết diện bằng nhau. Dây tóc của đèn nào có độ dài lớn hơn và lớn hơn bao nhiêu lần?
