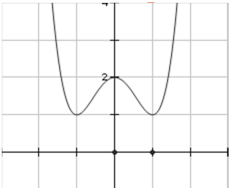
Cho hàm số y=f(x) có đồ thị như hình vẽ.
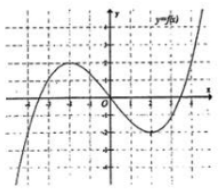
Tìm số nghiệm thuộc \(\left[-\frac{\pi}{6} ; \frac{5 \pi}{6}\right]\) của phương trình \(f(2 \sin x+2)=1 ?\)
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(t=2 \sin x+2, x \in\left[-\frac{\pi}{6} ; \frac{5 \pi}{6}\right] \Rightarrow t \in\left[-\frac{1}{2} ; 1\right]\)
Khi đó: \(f(2 \sin x+2)=1 \Rightarrow f(t)=1\)
số nghiệm của phương trình f(t)=1 là số giao điểm của đồ thị hai hàm số y=f(t) và y=1.
Dựa vào đồ thị hàm số suy ra phương trình f(t)=1 không có nghiệm thực \( t \in\left[-\frac{1}{2} ; 1\right]\), hay phương trình \(f(2 \sin x+2)=1 \) không có nghiệm thuộc \(\left[-\frac{\pi}{6} ; \frac{5 \pi}{6}\right]\)
Câu hỏi liên quan
-
Cho hàm số y=f(x) có đồ thị như đường cong hình dưới. Phương trình f(x )=1 có bao nhiêu nghiệm ?
-
Có bao nhiêu điểm M thuộc đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEaiabgUcaRiaaikdaaeaacaWG4bGaeyOeI0Ia % aGymaaaaaaa!3D48! y = \frac{{x + 2}}{{x - 1}}\) sao cho khoảng cách từ M đến trục tung bằng hai lần khoảng cách từ M đến trục hoành.
-
Với m > 0 phương trình \(\left| x \right| = \sqrt[3]{{2{x^2} - \left| x \right| + m - 1}}\) có ít nhất mấy nghiệm?
-
Một cái hộp có dạng hình hộp chữ nhật có thể tích bằng 48 và chiều dài gấp đôi chiều rộng. Chất liệu làm đáy và 4 mặt bên của hộp có giá thành gấp ba lần giá thành của chất liệu làm nắp hộp. Gọi hh là chiều cao của hộp để giá thành của hộp là thấp nhất. Biết \( h = \frac{m}{n}\)với m, n là các số nguyên dương nguyên tố cùng nhau. Tổng m+n là
-
Cho hàm số \(y=\frac{2x-1}{x-1}\)có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số \(y=|\frac{2x-1}{x-1}|\)?
.png)
-
Cho đồ thị \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WGdbaacaGLOaGaayzkaaGaaiOoaiaaykW7caaMc8UaamyEaiabg2da % 9maalaaabaGaamiEaiabgkHiTiaaiodaaeaacaWG4bGaey4kaSIaaG % ymaaaaaaa!436D! \left( C \right):\,\,y = \frac{{x - 3}}{{x + 1}}\). Biết rằng, có hai điểm phân biệt thuộc đồ thị (C) và cách đều hai trục toạ độ. Giả sử các điểm đó lần lượt là M và N. Tìm độ dài của đoạn thẳng MN.
-
Cho hàm số \(y = \frac{3}{{x + 1}}\) có đồ thị (C). Mệnh đề nào sau đây là mệnh đề sai?
-
Cho hàm số y = x3 + x – 2 có đồ thị (C). Tìm tọa độ giao điểm của (C) và trục tung
-
Đồ thị hàm số \(y = \frac{{3{x^2} - 4x + 1}}{{x - 1}}\)
-
Đồ thị hàm số nào sau đây có hình dạng như hình vẽ bên
-
Bảng biến thiên sau đây là của hàm số nào?
-
Đồ thị sau đây là của hàm số nào ?
-
Phát biểu nào sau đây là đúng?
-
Đồ thị ở hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?
-
Cho hàm số f có đạo hàm trên khoảng I. Xét các mệnh đề sau:
(I). Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyyzImRaaGimaaaa!3BF1! f'\left( x \right) \ge 0\), \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyiaIiIaam % iEaiabgIGiolaadMeaaaa!3A13! \forall x \in I\) (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I) thì hàm số đồng biến trên I.
(II). Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyizImQaaGimaaaa!3BE0! f'\left( x \right) \le 0\),\(\forall x \in I\) (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I) thì hàm số nghịch biến trên I.
(III). Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyizImQaaGimaaaa!3BE0! f'\left( x \right) \le 0; \forall x \in I\) thì hàm số nghịch biến trên khoảng I.
(IV). Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyizImQaaGimaaaa!3BE0! f'\left( x \right) \le 0, \forall x \in I\) và f'(x) = 0 tại vô số điểm trên I thì hàm số f không thể nghịch biến trên khoảng I.
Trong các mệnh đề trên. Mệnh đề nào đúng, mệnh đề nào sai?
-
Số giao điểm của đồ thị hàm số \(y=\frac{x^{2}-4 x+3}{x+2}\)và trục hoành là
-
Cho đồ thị hàm số f(x) như hình bên. Hàm số nào dưới đây tương ứng với đồ thị đó?
-
Biết đồ thị hàm số \( y = \frac{{2x - 1}}{{x + 3}}\) cắt trục Ox,Oy lần lượt tại hai điểm phân biệt A, B. Tính diện tích S của tam giác OAB
-
Tìm giá trị của tham số m để hàm số\(y = - \dfrac{1}{3}({m^2} + 6m){x^3} - 2m{x^2} + 3x + 1\) đạt cực đại tại x = - 1.
-
Đường cong trong hình là đồ thị của một trong 4 hàm số được cho bởi các phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào?
