ADMICRO
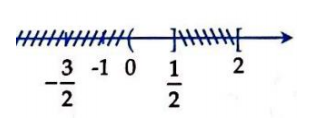
Cho 3 tập hợp . Tìm m để
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ZUNIA12
Lời giải:
Báo sai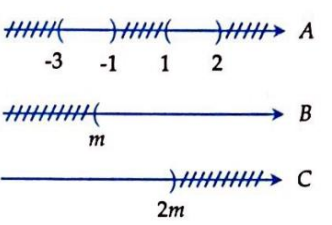
Trước tiên ta tìm m để
TH1: Nếu
TH2: Nếu
Vì
ZUNIA9
AANETWORK



.PNG)











