Biết $% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaabm % aabaGaamiEamaaBaaaleaacaWGbbaabeaakiaacUdacaaMc8UaamyE % amaaBaaaleaacaWGbbaabeaaaOGaayjkaiaawMcaaaaa!3E80! A\left( {{x_A};\,{y_A}} \right)$,$% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqamaabm % aabaGaamiEamaaBaaaleaacaWGcbaabeaakiaacUdacaaMc8UaamyE % amaaBaaaleaacaWGcbaabeaaaOGaayjkaiaawMcaaaaa!3E83! B\left( {{x_B};\,{y_B}} \right)$  là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số $% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqamaabm % aabaGaamiEamaaBaaaleaacaWGcbaabeaakiaacUdacaaMc8UaamyE % amaaBaaaleaacaWGcbaabeaaaOGaayjkaiaawMcaaaaa!3E83! B\left( {{x_B};\,{y_B}} \right)$ sao cho đoạn thẳng AB có độ dài nhỏ nhất. Tính $% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuaiabg2 % da9iaadIhadaqhaaWcbaGaamyqaaqaaiaaikdaaaGccqGHRaWkcaWG % 4bWaa0baaSqaaiaadkeaaeaacaaIYaaaaOGaey4kaSIaamyEamaaBa % aaleaacaWGbbaabeaakiaac6cacaWG5bWaaSbaaSqaaiaadkeaaeqa % aaaa!439D! P = x_A^2 + x_B^2 + {y_A}.{y_B}$.

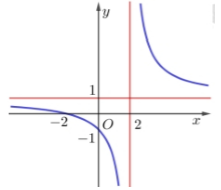
Đồ thị (C) của $% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEaiabgUcaRiaaigdaaeaacaWG4bGaeyOeI0Ia % aGymaaaaaaa!3D47! y = \frac{{x + 1}}{{x - 1}}$ có tiệm cận đứng x =1 và tiệm cận ngang y =1, gọi  I(1;1) là giao điểm của hai đường tiệm cận; (I)  là tâm đối xứng của (C).

Giả sử A thuộc nhánh phải của đồ thị $% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % yqamaabmaabaGaamyyaiabgUcaRiaaigdacaGG7aGaaGPaVpaalaaa % baGaamyyaiabgUcaRiaaikdaaeaacaWGHbaaaaGaayjkaiaawMcaaa % aa!42E7! \Rightarrow A\left( {a + 1;\,\frac{{a + 2}}{a}} \right), a > 0$

B thuộc nhánh trái đồ thị $% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % OqamaabmaabaGaaGymaiabgkHiTiaadkgacaGG7aWaaSaaaeaacaWG % IbGaeyOeI0IaaGOmaaqaaiaadkgaaaaacaGLOaGaayzkaaaaaa!4176! \Rightarrow B\left( {1 - b;\frac{{b - 2}}{b}} \right); b > 0$

$% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8Haaeaaca % WGcbGaamyqaaGaay51GaGaeyypa0ZaaeWaaeaacaWGHbGaey4kaSIa % amOyaiaacUdacaaMc8+aaSaaaeaacaaIYaWaaeWaaeaacaWGHbGaey % 4kaSIaamOyaaGaayjkaiaawMcaaaqaaiaadggacaWGIbaaaaGaayjk % aiaawMcaaaaa!478E! \overrightarrow {BA} = \left( {a + b;\,\frac{{2\left( {a + b} \right)}}{{ab}}} \right)$$% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % yqaiaadkeadaahaaWcbeqaaiaaikdaaaGccqGH9aqpdaqadaqaaiaa % dggacqGHRaWkcaWGIbaacaGLOaGaayzkaaWaaWbaaSqabeaacaaIYa % aaaOGaey4kaSYaaSaaaeaacaaI0aWaaeWaaeaacaWGHbGaey4kaSIa % amOyaaGaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaOqaamaabm % aabaGaamyyaiaadkgaaiaawIcacaGLPaaadaahaaWcbeqaaiaaikda % aaaaaaaa!4C1C! \Rightarrow A{B^2} = {\left( {a + b} \right)^2} + \frac{{4{{\left( {a + b} \right)}^2}}}{{{{\left( {ab} \right)}^2}}}$

$% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyaiaadk % gacqGHKjYOdaWcaaqaamaabmaabaGaamyyaiabgUcaRiaadkgaaiaa % wIcacaGLPaaadaahaaWcbeqaaiaaikdaaaaakeaacaaI0aaaaaaa!3F6F! ab \le \frac{{{{\left( {a + b} \right)}^2}}}{4}$$% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H49aae % WaaeaacaWGHbGaamOyaaGaayjkaiaawMcaamaaCaaaleqabaGaaGOm % aaaakiabgsMiJoaalaaabaWaaeWaaeaacaWGHbGaey4kaSIaamOyaa % GaayjkaiaawMcaamaaCaaaleqabaGaaGinaaaaaOqaaiaaigdacaaI % 2aaaaaaa!4507! \Rightarrow {\left( {ab} \right)^2} \le \frac{{{{\left( {a + b} \right)}^4}}}{{16}}$

$% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % yqaiaadkeadaahaaWcbeqaaiaaikdaaaGccqGHLjYSdaqadaqaaiaa % dggacqGHRaWkcaWGIbaacaGLOaGaayzkaaWaaWbaaSqabeaacaaIYa % aaaOGaey4kaSYaaSaaaeaacaaI2aGaaGinaaqaamaabmaabaGaamyy % aiabgUcaRiaadkgaaiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaa % aaaOGaeyyzImRaaGOmamaakaaabaGaaGOnaiaaisdaaSqabaGccqGH % 9aqpcaaIXaGaaGOnaaaa!5003! \Rightarrow A{B^2} \ge {\left( {a + b} \right)^2} + \frac{{64}}{{{{\left( {a + b} \right)}^2}}} \ge 2\sqrt {64} = 16$$% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % yqaiaadkeacqGHLjYScaaI0aaaaa!3C62! \Rightarrow AB \ge 4$

Dấu "=" xảy ra $% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aai % qaaqaabeqaaiaadggacqGH9aqpcaWGIbaabaWaaeWaaeaacaWGHbGa % ey4kaSIaamOyaaGaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaaki % abg2da9iaaiIdaaaGaay5Eaaaaaa!4337! \Leftrightarrow \left\{ \begin{array}{l} a = b\\ {\left( {a + b} \right)^2} = 8 \end{array} \right.$$% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % yyaiabg2da9iaadkgacqGH9aqpdaGcaaqaaiaaikdaaSqabaaaaa!3D00! \Leftrightarrow a = b = \sqrt 2$

$% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % yqamaabmaabaGaaGymaiabgUcaRmaakaaabaGaaGOmaaWcbeaakiaa % cUdacaaMc8UaaGymaiabgUcaRmaakaaabaGaaGOmaaWcbeaaaOGaay % jkaiaawMcaaaaa!41E6! \Rightarrow A\left( {1 + \sqrt 2 ;\,1 + \sqrt 2 } \right)$$% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqamaabm % aabaGaaGymaiabgkHiTmaakaaabaGaaGOmaaWcbeaakiaacUdacaaM % c8UaaGymaiabgkHiTmaakaaabaGaaGOmaaWcbeaaaOGaayjkaiaawM % caaaaa!3FA0! ;B\left( {1 - \sqrt 2 ;\,1 - \sqrt 2 } \right)$

Vậy $% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuaiabg2 % da9iaadIhadaqhaaWcbaGaamyqaaqaaiaaikdaaaGccqGHRaWkcaWG % 4bWaa0baaSqaaiaadkeaaeaacaaIYaaaaOGaey4kaSIaamyEamaaBa % aaleaacaWGbbaabeaakiaac6cacaWG5bWaaSbaaSqaaiaadkeaaeqa % aOGaeyypa0JaaGynaaaa!456C! P = x_A^2 + x_B^2 + {y_A}.{y_B} = 5$