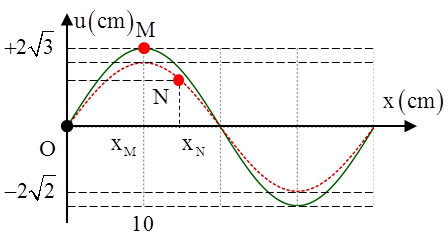
Sóng dừng trên một sợi dây với biên độ điểm bụng là 4 cm. Hình vẽ biểu diễn hình dạng của sợi dây ở thời điểm t1 (nét liền) và t2 (nét đứt). Ở thời điểm t1 điểm bụng M đang di chuyển với tốc độ bằng tốc độ của điểm N ở thời điểm t2. Tọa độ của điểm N ở thời điểm t2 là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có M và N thuộc vùng một bó sóng nên dao động cùng pha với nhau.
Dựa vào đồ thị, ta có: \(\frac{\lambda }{4}=10\text{ cm}\Rightarrow \lambda =40\text{ cm}\text{.}\)
Tại thời điểm t1, ta có: \({{u}_{M}}={{A}_{M}}.cos{{\varphi }_{1}}=4cos{{\varphi }_{1}}=2\sqrt{3}\text{ cm}\Rightarrow cos{{\varphi }_{1}}=\frac{\sqrt{3}}{2}.\)
\(\Rightarrow \sin {{\varphi }_{1}}=\sqrt{1-co{{s}^{2}}{{\varphi }_{1}}}=\frac{1}{2}.\)
Vận tốc của điểm M tại thời điểm t1 là \[{{v}_{M}}=-\omega .A.\sin {{\varphi }_{1}}=-\omega .4.\frac{1}{2}=-2\omega \text{ cm/s}\text{.}\]
Tại thời điểm t2, ta có: \({{u}_{M}}={{A}_{M}}.cos{{\varphi }_{2}}=4cos{{\varphi }_{2}}=2\sqrt{2}\text{ cm}\Rightarrow cos{{\varphi }_{2}}=\frac{1}{\sqrt{2}}.\)
\(\Rightarrow \sin {{\varphi }_{2}}=\sqrt{1-co{{s}^{2}}{{\varphi }_{2}}}=\frac{1}{\sqrt{2}}.\)
Vận tốc của điểm N tại thời điểm t2 là \[{{v}_{N}}=-\omega .{{A}_{N}}.\sin {{\varphi }_{2}}=-\omega .{{A}_{N}}.\frac{1}{\sqrt{2}}=-\frac{{{A}_{N}}}{\sqrt{2}}.\omega \text{ cm/s}\text{.}\]
Theo đề bài, ta có: \[-\frac{{{A}_{N}}}{\sqrt{2}}.\omega =-2\omega \Rightarrow {{A}_{N}}=2\sqrt{2}\text{ cm}\text{.}\]
Vậy tại thời điểm t2, ta có \({{u}_{N}}={{A}_{N}}.cos{{\varphi }_{2}}=2\sqrt{2}.\frac{1}{\sqrt{2}}=2\text{ cm}\text{.}\)
Mặt khác, ta có \(\frac{{{A}_{N}}}{{{A}_{M}}}=\frac{1}{\sqrt{2}}\Rightarrow {{A}_{N}}=\frac{A}{\sqrt{2}}\) với A là biên độ bụng sóng => N cách bụng sóng một khoảng \(\frac{\lambda }{8}=\frac{40}{8}=5\text{ cm}\text{.}\)
Vậy xN = xM + 5 = 10 + 5 = 15 cm.