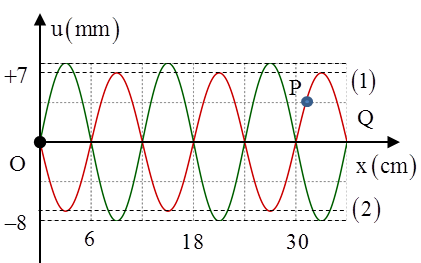
Trên sợi dây OQ căng ngang, hai đầu cố định đang có sóng dừng với tần số f xác định. Hình vẽ mô tả hình dạng sợi dây tại thời điểm t1 (đường 1), \({{t}_{2}}={{t}_{1}}+\frac{1}{6f}\) (đường 2) và P là một phần tử trên dây. Tỉ số tốc độ truyền sóng trên dây và tốc độ dao động cực đại của phần tử P xấp xỉ bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiDựa vào đồ thị, ta có λ = 12 cm.
Ta có: \({{t}_{2}}={{t}_{1}}+\frac{1}{6f}={{t}_{1}}+\frac{T}{6}\Rightarrow\) từ thời điểm t1 và t2 ứng với góc quét là \(\frac{\pi }{3}.\)

Ta có hình vẽ, xét tại điểm bụng:
\(\left\{ \begin{align} & \sin \alpha =\frac{7}{A} \\ & \cos \beta =\frac{8}{A} \\ \end{align} \right.\xrightarrow{\alpha +\beta =\frac{\pi }{3}}\cos \left( \alpha +\beta \right)=\frac{1}{2}.\)
Khai triển lượng giác, ta có:
\(\text{ }\cos \left( \alpha +\beta \right)=\cos \alpha .\cos \beta -\sin \alpha .\sin \beta =\frac{1}{2}$\)
\(\Leftrightarrow \sqrt{\left( 1-\frac{49}{{{A}^{2}}} \right)\left( 1-\frac{64}{{{A}^{2}}} \right)}-\left( \frac{7}{A} \right).\frac{8}{A}=\frac{1}{2}\)
\(\Leftrightarrow \sqrt{1-\frac{113}{{{A}^{2}}}+\frac{3136}{{{A}^{4}}}}=\frac{1}{2}+\frac{56}{{{A}^{2}}}\)
\(\Leftrightarrow 1-\frac{113}{{{A}^{2}}}+\frac{3136}{{{A}^{4}}}=\frac{1}{4}+\frac{56}{{{A}^{2}}}+\frac{3136}{{{A}^{4}}}\)
\(\Leftrightarrow A=\frac{26}{\sqrt{3}}\text{ mm}\text{.}\)
Tại thời điểm t1 P có li độ là 4 mm và điểm bụng có li độ 7 mm nên \(\frac{{{A}_{P}}}{A}=\frac{4}{7}\Rightarrow {{A}_{P}}=\frac{104}{7\sqrt{3}}\text{ mm}\text{.}\)
Tỉ số vận tốc: \(\delta =\frac{v}{\omega .{{A}_{P}}}=\frac{\lambda .f}{2\pi f.{{A}_{P}}}=\frac{120}{2\pi .{{A}_{P}}}\approx 2,2.\)














